第40页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
观察图中尺规作图的痕迹,可得线段BD一定是△ABC的(
A.角平分线
B.高线
C.中位线
D.中线
B
)A.角平分线
B.高线
C.中位线
D.中线
答案:
1 B
2 [2023南京中考]若一个等腰三角形的腰长为3,则它的周长可能是(
A.5
B.10
C.15
D.20
B
)A.5
B.10
C.15
D.20
答案:
2 B
∵等腰三角形的腰长为3,
∴3 - 3 < 等腰三角形的底边长 < 3 + 3,即0 < 等腰三角形的底边长 < 6,
∴6 < 等腰三角形的周长 < 12.
∵等腰三角形的腰长为3,
∴3 - 3 < 等腰三角形的底边长 < 3 + 3,即0 < 等腰三角形的底边长 < 6,
∴6 < 等腰三角形的周长 < 12.
3 [2024云南中考]已知AF是等腰三角形ABC底边BC上的高,若点F到直线AB的距离为3,则点F到直线AC的距离为( )
A.$\frac{3}{2}$
B.2
C.3
D.$\frac{7}{2}$
A.$\frac{3}{2}$
B.2
C.3
D.$\frac{7}{2}$
答案:
3 C 如图,
∵AF是等腰三角形ABC底边BC上的高,
∴AF平分∠BAC,
∴点F到直线AB,AC的距离相等.
∵点F到直线AB的距离为3,
∴点F到直线AC的距离为3.

3 C 如图,
∵AF是等腰三角形ABC底边BC上的高,
∴AF平分∠BAC,
∴点F到直线AB,AC的距离相等.
∵点F到直线AB的距离为3,
∴点F到直线AC的距离为3.

4 [2024内江中考]如图,在△ABC中,∠DCE= 40°,AE= AC,BC= BD,则∠ACB的度数为______.
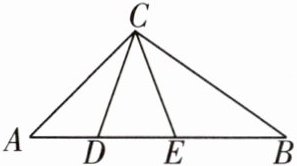

100°
答案:
4 100°
∵∠DCE=40°,
∴∠CDE + ∠CED=180° - ∠DCE=140°.
∵AE=AC,BC=BD,
∴∠ACE=∠AEC,∠BCD=∠BDC,
∴∠ACE + ∠BCD=∠CED + ∠CDE=140°,
∴∠ACB=∠ACE + ∠BCE=∠ACE + ∠BCD - ∠DCE=140° - 40°=100°.
∵∠DCE=40°,
∴∠CDE + ∠CED=180° - ∠DCE=140°.
∵AE=AC,BC=BD,
∴∠ACE=∠AEC,∠BCD=∠BDC,
∴∠ACE + ∠BCD=∠CED + ∠CDE=140°,
∴∠ACB=∠ACE + ∠BCE=∠ACE + ∠BCD - ∠DCE=140° - 40°=100°.
5 [2024辽宁中考]如图,四边形ABCD中,AD//BC,AD>AB,AD= a,AB= 10,以点A为圆心,AB的长为半径作弧,与BC相交于点E,连接AE.以点E为圆心,适当长为半径作弧,分别与EA,EC相交于点M,N,再分别以点M,N为圆心,大于$\frac{1}{2}$MN的长为半径作弧,两弧在∠AEC的内部相交于点P,作射线EP,与AD相交于点F,则FD的长为______.(用含a的代数式表示)
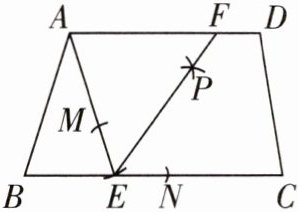

a - 10
答案:
5 a - 10 由作法,得AE=AB=10,EF平分∠AEC,
∴∠AEF=∠CEF.
∵AD//BC,
∴∠AFE=∠CEF,
∴∠AEF=∠AFE,
∴AF=AE=10,
∴FD=AD - AF=a - 10.
∴∠AEF=∠CEF.
∵AD//BC,
∴∠AFE=∠CEF,
∴∠AEF=∠AFE,
∴AF=AE=10,
∴FD=AD - AF=a - 10.
6 [2024绥化中考]如图,已知∠AOB= 50°,点P为∠AOB内部一点,点M为射线OA、点N为射线OB上的两个动点,当△PMN的周长最小时,则∠MPN= ______°.
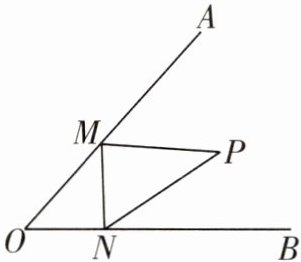

答案:
6 80 如图,作点P关于OA,OB的对称点P₁,P₂,连接OP₁,OP₂,P₁P₂,则当M,N是P₁P₂与OA,OB的交点时,△PMN的周长最小,连接P₁P,P₂P.
∵点P,P₁关于OA对称,
∴∠P₁OP=2∠MOP,OP₁=OP,P₁M=PM,∠OP₁M=∠OPM.同理,∠P₂OP=2∠NOP,OP=OP₂,∠OP₂N=∠OPN,
∴∠P₁OP₂=∠P₁OP + ∠P₂OP=2(∠MOP + ∠NOP)=2∠AOB=100°,OP₁=OP₂=OP,
∴△P₁OP₂是等腰三角形,
∴∠OP₂N=∠OP₁M=40°,
∴∠MPN=∠MPO + ∠NPO=∠OP₁M + ∠OP₂N=80°.

6 80 如图,作点P关于OA,OB的对称点P₁,P₂,连接OP₁,OP₂,P₁P₂,则当M,N是P₁P₂与OA,OB的交点时,△PMN的周长最小,连接P₁P,P₂P.
∵点P,P₁关于OA对称,
∴∠P₁OP=2∠MOP,OP₁=OP,P₁M=PM,∠OP₁M=∠OPM.同理,∠P₂OP=2∠NOP,OP=OP₂,∠OP₂N=∠OPN,
∴∠P₁OP₂=∠P₁OP + ∠P₂OP=2(∠MOP + ∠NOP)=2∠AOB=100°,OP₁=OP₂=OP,
∴△P₁OP₂是等腰三角形,
∴∠OP₂N=∠OP₁M=40°,
∴∠MPN=∠MPO + ∠NPO=∠OP₁M + ∠OP₂N=80°.

7 [2024常州中考]如图,B,E,C,F是直线l上的四点,AC,DE相交于点G,AB= DF,AC= DE,BC= EF.
(1)求证:△GEC是等腰三角形.
(2)连接AD,则AD与l的位置关系是
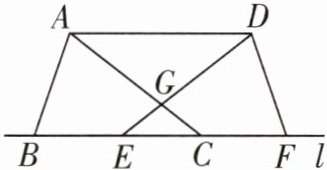
(1)求证:△GEC是等腰三角形.
(2)连接AD,则AD与l的位置关系是
AD//l
.
答案:
7
(1)证明:在△ABC和△DFE中,{AB=DF,AC=DE,BC=FE,
∴△ABC≌△DFE,
∴∠ACB=∠DEF,
∴EG=CG,
∴△GEC是等腰三角形.
(2)解:AD//l
∵AC=DE,EG=CG,
∴AC - CG=DE - EG,
∴AG=DG,
∴∠GAD=∠GDA=1/2(180° - ∠AGD).
∵∠ACE=∠DEF=1/2(180° - ∠CGE),∠AGD=∠EGC,
∴∠CAD=∠ACB,
∴AD//l.
(1)证明:在△ABC和△DFE中,{AB=DF,AC=DE,BC=FE,
∴△ABC≌△DFE,
∴∠ACB=∠DEF,
∴EG=CG,
∴△GEC是等腰三角形.
(2)解:AD//l
∵AC=DE,EG=CG,
∴AC - CG=DE - EG,
∴AG=DG,
∴∠GAD=∠GDA=1/2(180° - ∠AGD).
∵∠ACE=∠DEF=1/2(180° - ∠CGE),∠AGD=∠EGC,
∴∠CAD=∠ACB,
∴AD//l.
查看更多完整答案,请扫码查看


