《2025年一遍过八年级数学上册苏科版》

7 如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B.下列结论不成立的是(D)

A.PA= PB
B.PO平分∠APB
C.OA= OB
D.OA= OP

答案： D 因为PA⊥OA，PB⊥OB，所以∠OAP=∠OBP=90°。因为OP平分∠AOB，所以∠AOP=∠BOP。又因为OP=OP，所以△AOP≌△BOP(AAS)，所以PA=PB，OA=OB，∠APO=∠BPO，所以PO平分∠APB，所以A，B，C中的结论均成立，D中的结论不成立。

8 如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D,E,AD,CE交于点H.已知EH= EB= 3,AE= 4,则CH的长是(A)

A.1
B.2
C.3
D.4

答案： A
∵CE⊥AB，AD⊥BC，
∴∠AEH=∠ADB=90°，
∴∠EAH+∠AHE=90°，∠DHC+∠BCH=90°。又
∵∠EHA=∠DHC，
∴∠EAH=∠DCH。在△BCE和△HAE中，∠BCE=∠HAE，∠BEC=∠HEA，BE=HE，
∴△BCE≌△HAE(AAS)，
∴CE=AE=4。
∵EH=EB=3，
∴CH=CE - EH = 4 - 3 = 1。

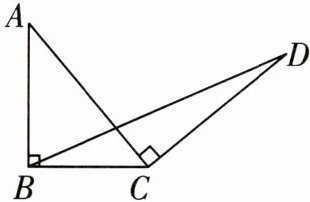
9 如图,∠ABC= ∠ACD= 90°,BC= 5,AC= CD,则△BCD的面积为______.

答案：
12.5 解题思路：作DH⊥BC，证明△ABC≌△CHD，然后根据全等三角形的性质，得DH=BC=5，再根据三角形的面积公式计算，得到答案。如图，过点D作DH⊥BC，交BC的延长线于点H。
∵∠ABC=90°，
∴∠BAC+∠ACB=90°。
∵∠ACD=90°，
∴∠HCD+∠ACB=90°，
∴∠BAC=∠HCD。在△ABC和△CHD中，∠ABC=∠CHD，∠BAC=∠HCD，AC=CD，
∴△ABC≌△CHD(AAS)，
∴DH=BC=5，
∴△BCD的面积为$\frac{1}{2}$BC·DH = $\frac{1}{2}$×5×5 = 12.5。

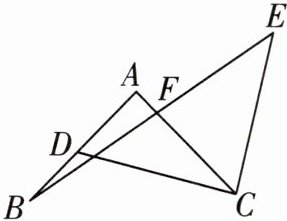
10 [2025北师大实验中学期中]如图,AB⊥AC,AB= AC,D是AB上一点,CE⊥CD,CE= CD,连接BE交AC于点F.求证：F是BE的中点.

答案：
证明：如图，过点E作EH⊥AC于点H，则∠EHC=∠EHF=90°。
∵AB⊥AC，
∴∠DAC=90°，
∴∠ADC+∠ACD=90°。
∵CE⊥CD，
∴∠ECH+∠ACD=90°，
∴∠ECH=∠CDA。在△HEC和△ACD中，∠EHC=∠CAD，∠ECH=∠CDA，CE=DC，
∴△HEC≌△ACD(AAS)，
∴EH=AC。
∵AB=AC，
∴EH=AB。在△ABF和△HEF中，∠AFB=∠HFE，∠BAF=∠EHF，AB=HE，
∴△ABF≌△HEF(AAS)，
∴BF=EF，
∴F是BE的中点。

(1)【初步探究】请你探究线段DE,BD,CE之间的数量关系.
CE=BD+DE
(2)【全等模型】如图2,在△ABC中,∠BAC= 90°,AB= AC,直线l经过点A,BD⊥直线l,CE⊥直线l,垂足分别为D,E,则DE,BD,CE之间的数量关系为______.
DE=BD+CE
(3)【类比探究】如图3,在△ABC中,AB= AC,直线MN经过点A,E,D,且∠BDM= ∠BAC= ∠DEC,请判断DE,BD,CE之间的数量关系,并说明理由.
CE=DE+BD。理由如下：
∵∠BDM=∠BAC=∠DEC，
∴180° - ∠BDM=180° - ∠DEC，∠BDM=∠ABD+∠BAD，
∴∠ADB=∠CEA。
∵∠BAC=∠BAD+∠CAE，
∴∠ABD+∠BAD=∠BAD+∠CAE，
∴∠ABD=∠CAE。在△ABD和△CAE中，∠ADB=∠CEA，∠ABD=∠CAE，AB=CA，
∴△ABD≌△CAE(AAS)，
∴AD=CE，BD=AE。
∵AD=DE+AE，
∴CE=DE+BD。
(4)归纳上述(1)(2)(3),请用简洁的语言表述DE,BD,CE的关系.
当点B，C在AE同侧时，DE=BD+CE；当点B，C在AE异侧时，CE=DE+BD。

答案： 解：
(1)
∵OB⊥OC，
∴∠BOD+∠COE=90°。
∵CE⊥OA，BD⊥OA，
∴∠CEO=∠ODB=90°，
∴∠BOD+∠B=90°，
∴∠COE=∠B。在△COE和△OBD中，∠CEO=∠ODB，∠COE=∠B，OC=BO，
∴△COE≌△OBD(AAS)，
∴OE=BD，CE=OD。
∵OD=OE+DE，
∴CE=BD+DE。
(2)DE=BD+CE
∵BD⊥直线l，CE⊥直线l，
∴∠ADB=∠CEA=90°，
∴∠CAE+∠ACE=90°。
∵∠BAC=90°，
∴∠BAD+∠CAE=90°，
∴∠ACE=∠BAD。在△ABD和△CAE中，∠ADB=∠CEA，∠BAD=∠ACE，AB=CA，
∴△ABD≌△CAE(AAS)，
∴BD=AE，AD=CE，
∴DE=AE+AD=BD+CE，即DE=BD+CE。
(3)CE=DE+BD。理由如下：
∵∠BDM=∠BAC=∠DEC，
∴180° - ∠BDM=180° - ∠DEC，∠BDM=∠ABD+∠BAD，
∴∠ADB=∠CEA。
∵∠BAC=∠BAD+∠CAE，
∴∠ABD+∠BAD=∠BAD+∠CAE，
∴∠ABD=∠CAE。在△ABD和△CAE中，∠ADB=∠CEA，∠ABD=∠CAE，AB=CA，
∴△ABD≌△CAE(AAS)，
∴AD=CE，BD=AE。
∵AD=DE+AE，
∴CE=DE+BD。
(4)归纳
(1)
(2)
(3)，结论可表述为：当点B，C在AE同侧时，DE=BD+CE；当点B，C在AE异侧时，CE=DE+BD。