第33页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
1 一题多解 如图,$AB// CD$,$\triangle ACE$为等边三角形,$∠DCE = 40^{\circ}$,则$∠EAB$等于(
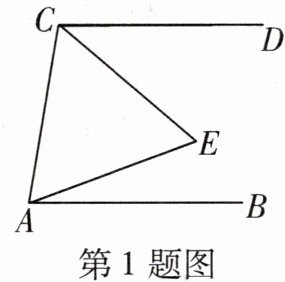
A.$40^{\circ}$
B.$30^{\circ}$
C.$20^{\circ}$
D.$15^{\circ}$
C
)
A.$40^{\circ}$
B.$30^{\circ}$
C.$20^{\circ}$
D.$15^{\circ}$
答案:
C
2 如图,在$\triangle ABC$中,$BC的垂直平分线分别交BC$,$AB于点E$,$F$。若$\triangle AFC$是等边三角形,则$∠B = $
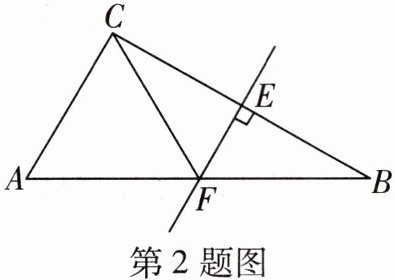
30
$^{\circ}$。
答案:
30
如图,在等边三角形$ABC$中,点$D$,$E分别在边BC$,$AC$上,$DE// AB$,过点$E作EF\perp DE$,交$BC的延长线于点F$。若$CF = 3$,则$CE$的长是
3
。
答案:
3
4 [2023荆州中考]如图,$BD是等边三角形ABC$的中线,以$D$点为圆心,$DB$的长为半径画弧,交$BC的延长线于点E$,连接$DE$。求证:$CD = CE$。
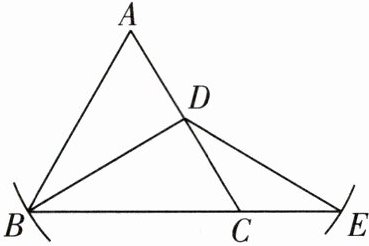

答案:
证明:
∵BD是等边三角形ABC的中线,
∴BD⊥AC,∠ACB=60°,
∴∠DBC=30°.
∵BD=DE,
∴∠E=∠DBC=30°.
∵∠CDE+∠E=∠ACB=60°,
∴∠E=∠CDE=30°,
∴CD=CE.
∵BD是等边三角形ABC的中线,
∴BD⊥AC,∠ACB=60°,
∴∠DBC=30°.
∵BD=DE,
∴∠E=∠DBC=30°.
∵∠CDE+∠E=∠ACB=60°,
∴∠E=∠CDE=30°,
∴CD=CE.
5 [2025扬州树人中学期末]数学知识的呈现一般表现出连贯性、一致性,所以在学习数学知识的过程中应该学会将新知识纳入已学的知识框架内,形成知识体系。例如,某同学在复习三角形时将几种三角形的关系整理如图,请帮他在括号内填上一个适当的条件:
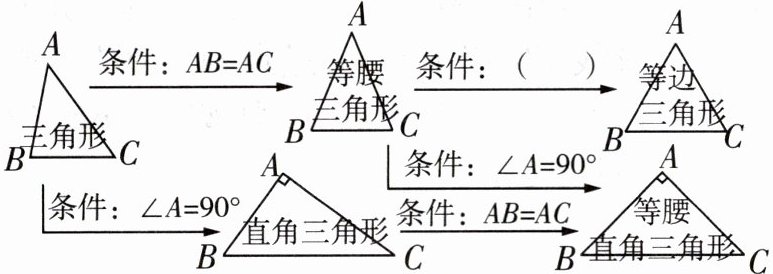
∠B=60°(答案不唯一)
。
答案:
∠B=60°(答案不唯一)
6 一题多解 如图,$AB = AC$,$DB = DC$,$∠ABC = 60^{\circ}$,$BE = 3cm$,则$AB = $

6
$cm$。
答案:
6
7 一题多解 如图,在$\triangle ABC$中,$AB = AC$,$D为AC$的中点,$DE\perp AB$,$DF\perp BC$,垂足分别为$E$,$F$,且$DE = DF$。求证:$\triangle ABC$是等边三角形。


答案:
证明:通解
∵AB=AC,
∴∠B=∠C.
∵DE⊥AB,DF⊥BC,
∴∠DEA=∠DFC=90°.
∵D为AC的中点,
∴DA=DC.又
∵DE=DF,
∴Rt△ADE≌Rt△CDF(HL),
∴∠A=∠C,
∴∠A=∠B=∠C,
∴△ABC是等边三角形.另解1 如图,连接BD.
∵DE⊥AB,DF⊥BC,
∴$S_{\triangle ABD}=\frac {1}{2}AB\cdot DE$,$S_{\triangle BCD}=\frac {1}{2}BC\cdot DF$.
∵D为AC的中点,
∴$S_{\triangle ABD}=S_{\triangle BCD}$,
∴$\frac {1}{2}AB\cdot DE=\frac {1}{2}BC\cdot DF$.又
∵DE=DF,
∴AB=BC.又
∵AB=AC,
∴AB=AC=BC,
∴△ABC是等边三角形. 另解2 如图,连接BD.
另解2 如图,连接BD.
∵DE⊥AB,DF⊥BC,DE=DF,
∴∠DBE=∠DBF.易证明△BDE≌△BDF(AAS)和Rt△ADE≌Rt△CDF(HL),从而BE=BF,AE=CF,进而可得BE+AE=BF+CF,即AB=BC.又
∵AB=AC,
∴AB=BC=AC,
∴△ABC是等边三角形.
证明:通解
∵AB=AC,
∴∠B=∠C.
∵DE⊥AB,DF⊥BC,
∴∠DEA=∠DFC=90°.
∵D为AC的中点,
∴DA=DC.又
∵DE=DF,
∴Rt△ADE≌Rt△CDF(HL),
∴∠A=∠C,
∴∠A=∠B=∠C,
∴△ABC是等边三角形.另解1 如图,连接BD.
∵DE⊥AB,DF⊥BC,
∴$S_{\triangle ABD}=\frac {1}{2}AB\cdot DE$,$S_{\triangle BCD}=\frac {1}{2}BC\cdot DF$.
∵D为AC的中点,
∴$S_{\triangle ABD}=S_{\triangle BCD}$,
∴$\frac {1}{2}AB\cdot DE=\frac {1}{2}BC\cdot DF$.又
∵DE=DF,
∴AB=BC.又
∵AB=AC,
∴AB=AC=BC,
∴△ABC是等边三角形.
 另解2 如图,连接BD.
另解2 如图,连接BD.∵DE⊥AB,DF⊥BC,DE=DF,
∴∠DBE=∠DBF.易证明△BDE≌△BDF(AAS)和Rt△ADE≌Rt△CDF(HL),从而BE=BF,AE=CF,进而可得BE+AE=BF+CF,即AB=BC.又
∵AB=AC,
∴AB=BC=AC,
∴△ABC是等边三角形.
8 [2025南京求真中学期中]如图,在$\triangle ABC$中,$∠ACB = 90^{\circ}$,$CD是边AB$上的高,$∠A = 30^{\circ}$。若$BD = 2$,则$AB$的长为______

8
。
答案:
8
9 如图,在$\triangle ABC$中,$AB = AC$,$∠BAC = 120^{\circ}$,$P是BC$上一点,且$∠BAP = 90^{\circ}$。
(1)求证:$PA = PC$。
(2)若$CP = 10$,求$BP$的长。

(1)求证:$PA = PC$。
(2)若$CP = 10$,求$BP$的长。

答案:
(1)证明:
∵AB=AC,∠BAC=120°,
∴∠B=∠C=$\frac {1}{2}(180^{\circ }-\angle BAC)=\frac {1}{2}×(180^{\circ }-120^{\circ })=30^{\circ }$.
∵∠BAP=90°,
∴∠PAC=∠BAC-∠BAP=120°-90°=30°,
∴∠PAC=∠C=30°,
∴PA=PC.
(2)解:由
(1)知PA=PC,且CP=10,
∴PA=10.又
∵在Rt△APB中,∠B=30°,
∴BP=2AP=20.
(1)证明:
∵AB=AC,∠BAC=120°,
∴∠B=∠C=$\frac {1}{2}(180^{\circ }-\angle BAC)=\frac {1}{2}×(180^{\circ }-120^{\circ })=30^{\circ }$.
∵∠BAP=90°,
∴∠PAC=∠BAC-∠BAP=120°-90°=30°,
∴∠PAC=∠C=30°,
∴PA=PC.
(2)解:由
(1)知PA=PC,且CP=10,
∴PA=10.又
∵在Rt△APB中,∠B=30°,
∴BP=2AP=20.
查看更多完整答案,请扫码查看


