《2025年一遍过八年级数学上册苏科版》

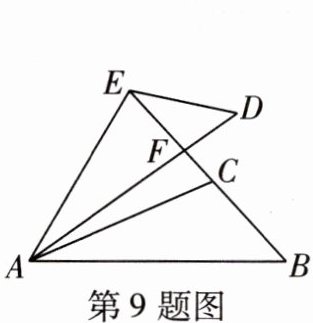
9 [2025无锡江阴期中]如图,$\triangle ABC \cong \triangle ADE$,线段$BC的延长线过点E$,与线段$AD交于点F$,$\angle ACB = \angle AED = 108^{\circ}$, $\angle CAD = 12^{\circ}$, $\angle B = 48^{\circ}$,则$\angle DEF$的度数为(B)

A.$28^{\circ}$
B.$36^{\circ}$
C.$38^{\circ}$
D.$42^{\circ}$

答案： B
∵∠ACB=108°,∠B=48°,
∴∠CAB=180° - ∠B - ∠ACB=180° - 48° - 108°=24°.又
∵△ABC≌△ADE,
∴∠EAD=∠CAB=24°.又
∵∠EAB=∠EAD+∠CAD+∠CAB,∠CAD=12°,
∴∠EAB=24°+12°+24°=60°,
∴∠AEB=180° - ∠EAB - ∠B=180° - 60° - 48°=72°,
∴∠DEF=∠AED - ∠AEB=108° - 72°=36°.

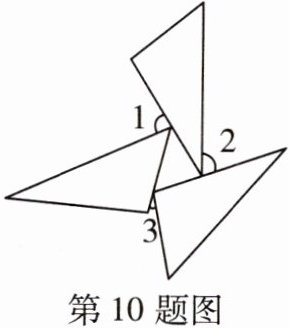
10 [2024南京二十九中月考]三个全等三角形按如图所示的方式摆放,则$\angle 1 + \angle 2 + \angle 3$的度数为( )

A.$90^{\circ}$
B.$120^{\circ}$
C.$135^{\circ}$
D.$180^{\circ}$

答案：
D 如图,△ABC的三个外角的和等于360°,即∠1+∠4+∠3+∠5+∠2+∠6=360°.因为∠4,∠5,∠6所在的三个三角形全等,且它们不互为对应角,所以∠4+∠5+∠6=180°,所以∠1+∠2+∠3=360° - 180°=180°.

11 如图,点$D$,$E$,$F分别在\triangle ABC的边AB$,$BC$,$CA$上(不与顶点重合),设$\angle BAC = \alpha$, $\angle FED = \theta$.若$\triangle BED \cong \triangle CFE$,则$\alpha$,$\theta$满足的关系是(B)
A.$\alpha + \theta = 90^{\circ}$
B.$\alpha + 2\theta = 180^{\circ}$
C.$\alpha - \theta = 90^{\circ}$
D.$2\alpha + \theta = 180^{\circ}$

答案： B
∵∠BAC=α,
∴∠B+∠C=180° - α.
∵△BED≌△CFE,
∴∠B=∠C=90° - $\frac{1}{2}$α,∠BDE=∠CEF,
∴∠BDE+∠BED=180° - ∠B=180° - (90° - $\frac{1}{2}$α)=90°+$\frac{1}{2}$α,
∴∠CEF+∠BED=90°+$\frac{1}{2}$α.
∵∠FED=θ,∠CEF+∠BED+∠FED=180°,
∴90°+$\frac{1}{2}$α+θ=180°,
∴α+2θ=180°.

12 如图是一个$3 × 3$的正方形网格,则$\angle 1 + \angle 2 + \angle 3 + \angle 4 = $180$^{\circ}$.

答案： 180
∵∠1和∠4所在的三角形全等,
∴∠1+∠4=90°.
∵∠2和∠3所在的三角形全等,
∴∠2+∠3=90°.
∴∠1+∠2+∠3+∠4=180°.

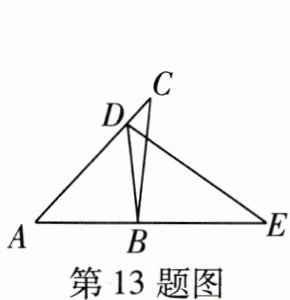
13 [2025南通张謇一中期末]如图,已知点$D在AC$上,点$B在AE$上,$\triangle ABC \cong \triangle DBE$,且$\angle BDA = \angle A$.若$\angle A:\angle C = 4:3$,则$\angle DBC = $12$^{\circ}$.

答案： 12
∵△ABC≌△DBE,
∴∠BDE=∠A=∠BDA,∠E=∠C.
∵∠A:∠C=4:3,
∴∠A:∠BDA:∠BDE:∠E=4:4:4:3.又
∵∠A+∠BDA+∠BDE+∠E=180°,
∴∠C=∠E=36°,∠BDE=∠A=∠BDA=48°,
∴∠ADE=180° - 48° - 36°=96°,
∴∠CDE=180° - 96°=84°,
∴∠DBC=180° - ∠C - ∠CDE - ∠BDE=180° - 36° - 84° - 48°=12°.

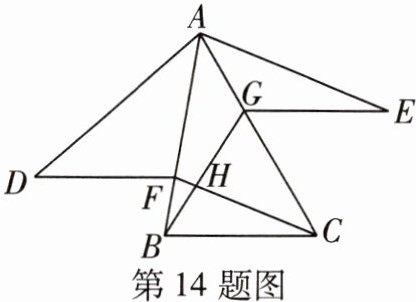
14 [2024扬州江都区八校联考]如图,在锐角三角形$ABC$中,$F$,$G分别是AB$,$AC$上的点,$\triangle ACF \cong \triangle ADF$, $\triangle ABG \cong \triangle AEG$,且$DF // BC // GE$,$BG$,$CF交于点H$.若$\angle BAC = 40^{\circ}$,则$\angle BHC$的度数为______.

答案：
100° 如图,延长EG交AD于点P.
∵△ACF≌△ADF,△ABG≌△AEG,∠BAC=40°,

∴∠DAF=∠BAC=40°,∠EAG=∠BAC=40°,∠D=∠ACF,∠E=∠ABG,
∴∠PAE=120°,
∴∠APE+∠E=60°.
∵DF//EP,
∴∠APE=∠D,
∴∠APE=∠ACF,
∴∠ABG+∠ACF=60°.
∵∠BFH=∠BAC+∠ACF,
∴∠BHC=∠ABG+∠BFH=∠ABG+∠BAC+∠ACF=60°+40°=100°.

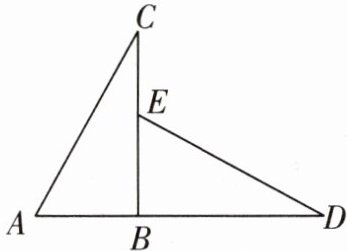
15 如图,$\triangle ABC \cong \triangle EBD$,$A$,$B$,$D$三点在一条直线上.
(1)通过怎样的变换方式,可以使$\triangle ABC与\triangle EBD$完全重合?
(2)判断线段$BC和AD$的位置关系,并说明理由.
(3)若$AD = 14$,$CE = 2$,求$BE$的长.

答案： 解:
(1)将△ABC绕点B顺时针旋转90°,可以与△EBD完全重合.
(2)BC⊥AD.理由如下:
∵△ABC≌△EBD,
∴∠ABC=∠EBD.
∵A,B,D三点在一条直线上,
∴∠ABC+∠EBD=180°,
∴∠ABC=∠EBD=90°,
∴BC⊥AD.
(3)
∵△ABC≌△EBD,
∴AB=EB,BC=BD,
∴AB=BE=BC - CE=BD - 2.
∵AD=14,
∴AB+BD=BD - 2+BD=14,
∴BD=8,
∴BE=6.

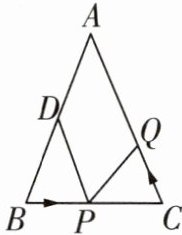
16 推理能力 如图,已知$\triangle ABC$中,$AB = AC = 10\mathrm{cm}$,$BC = 8\mathrm{cm}$,$D是AB$的中点,点$P在线段BC上以3\mathrm{cm/s}的速度由点B向点C$运动,同时点$Q在线段CA上以a\mathrm{cm/s}的速度由点C向点A$运动.设运动的时间为$t\mathrm{s}$.
(1)求$CP$的长(用含$t$的式子表示);
(2)若以点$C$,$P$,$Q为顶点的三角形和以点B$,$D$,$P$为顶点的三角形全等,并且$\angle B和\angle C$是对应角,求$a和t$的值.

答案：
解题思路:
解:
(1)由题意,得BP=3t cm.
∵BC=8 cm,
∴CP=(8 - 3t)cm.
(2)由题意,得BD=$\frac{1}{2}$AB=5 cm,BP=3t cm,CP=(8 - 3t)cm,CQ=at cm.
分两种情况:
①当△BDP≌△CPQ时,BD=CP,BP=CQ,
∴5=8 - 3t,3t=at,解得t=1,a=3.
②当△BDP≌△CQP时,BP=CP,BD=CQ,
∴3t=8 - 3t,5=at,解得t=$\frac{4}{3}$,a=$\frac{15}{4}$.
综上所述,a=3,t=1或a=$\frac{15}{4}$,t=$\frac{4}{3}$.
易错分析
混淆“≌”与“全等”的区别
当两个三角形用“≌”表示全等时,其对应顶点、对应边、对应角都唯一确定,但仅给出“全等”时,其对应关系不确定,要分类讨论.