第28页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
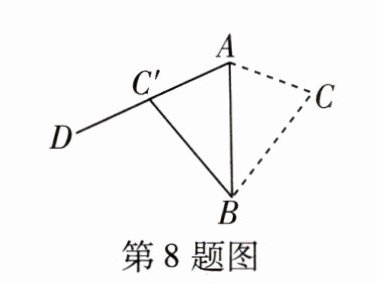
8 如图,△ABC的面积为6,AC= 3,现将△ABC沿AB所在直线翻折,使点C落在直线AD上的点C'处,P为直线AD上的一点,则线段BP的长不可能是( )
A.3
B.4
C.5.5
D.10

A.3
B.4
C.5.5
D.10
答案:
A 如图,过点B作$BN⊥AC$于点N,过点B作$BM⊥AD$于点M.由翻折知$∠C'AB=∠CAB$,所以AB是$∠DAC$的平分线,所以$BN=BM$.因为$△ABC$的面积等于6,$AC=3$,所以$\frac{1}{2}AC·BN=6$,所以$BN=4$,所以$BM=4$,所以点B到AD的最短距离是4. 结合各选项,知选项A符合题意.

A 如图,过点B作$BN⊥AC$于点N,过点B作$BM⊥AD$于点M.由翻折知$∠C'AB=∠CAB$,所以AB是$∠DAC$的平分线,所以$BN=BM$.因为$△ABC$的面积等于6,$AC=3$,所以$\frac{1}{2}AC·BN=6$,所以$BN=4$,所以$BM=4$,所以点B到AD的最短距离是4. 结合各选项,知选项A符合题意.

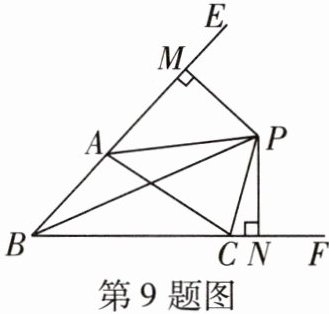
9 [2024南通启东折桂中学月考]如图,△ABC中,外角∠ACF,∠EAC的平分线CP,AP交于点P,PM⊥BE,PN⊥BF.下列结论中,正确的个数为( )
①BP平分∠ABC;②∠ABC+2∠APC= 180°;③∠CAB= 2∠CPB;④$S_{△PAC}= S_{△MAP}+S_{△NCP}$.
A.1
B.2
C.3
D.4
①BP平分∠ABC;②∠ABC+2∠APC= 180°;③∠CAB= 2∠CPB;④$S_{△PAC}= S_{△MAP}+S_{△NCP}$.

A.1
B.2
C.3
D.4
答案:
D 如图,过点P作$PQ⊥AC$于点Q.
∵$∠ACF,∠EAC$的平分线CP,AP交于点P,$PM⊥BE,PN⊥BF,\therefore PM=PQ,PQ=PN,\therefore PM=PN,\therefore$点P在$∠ABC$的平分线上,即BP平分$∠ABC$,故①正确.
∵$PM⊥BE,PN⊥BF,PQ⊥AC,\therefore ∠PMA=∠PQA=90^{\circ },∠PQC=∠PNC=90^{\circ }$.在$Rt△PMA$和$Rt△PQA$中,$\left\{\begin{array}{l} PA=PA,\\ PM=PQ,\end{array}\right. \therefore Rt△PMA\cong Rt△PQA,\therefore ∠MPA=∠QPA$.同理$Rt△PQC\cong Rt△PNC,\therefore ∠QPC=∠NPC.\because ∠PMA=∠PNC=90^{\circ },\therefore ∠ABC+∠MPN=360^{\circ }-90^{\circ }-90^{\circ }=180^{\circ },\therefore ∠ABC+2∠APC=180^{\circ }$,故②正确.
∵ CP平分$∠FCA$,BP平分$∠ABC,\therefore ∠FCA=∠ABC+∠CAB=2∠PCN$.又$\because ∠PCN=\frac{1}{2}∠ABC+∠CPB,\therefore ∠ABC+∠CAB=2(\frac{1}{2}∠ABC+∠CPB),\therefore ∠CAB=2∠CPB$,故③正确.
∵$Rt△PMA\cong Rt△PQA,Rt△PQC\cong Rt△PNC,\therefore S_{△PAC}=S_{△MAP}+S_{△NCP}$,故④正确.综上,正确的个数为4.

D 如图,过点P作$PQ⊥AC$于点Q.
∵$∠ACF,∠EAC$的平分线CP,AP交于点P,$PM⊥BE,PN⊥BF,\therefore PM=PQ,PQ=PN,\therefore PM=PN,\therefore$点P在$∠ABC$的平分线上,即BP平分$∠ABC$,故①正确.
∵$PM⊥BE,PN⊥BF,PQ⊥AC,\therefore ∠PMA=∠PQA=90^{\circ },∠PQC=∠PNC=90^{\circ }$.在$Rt△PMA$和$Rt△PQA$中,$\left\{\begin{array}{l} PA=PA,\\ PM=PQ,\end{array}\right. \therefore Rt△PMA\cong Rt△PQA,\therefore ∠MPA=∠QPA$.同理$Rt△PQC\cong Rt△PNC,\therefore ∠QPC=∠NPC.\because ∠PMA=∠PNC=90^{\circ },\therefore ∠ABC+∠MPN=360^{\circ }-90^{\circ }-90^{\circ }=180^{\circ },\therefore ∠ABC+2∠APC=180^{\circ }$,故②正确.
∵ CP平分$∠FCA$,BP平分$∠ABC,\therefore ∠FCA=∠ABC+∠CAB=2∠PCN$.又$\because ∠PCN=\frac{1}{2}∠ABC+∠CPB,\therefore ∠ABC+∠CAB=2(\frac{1}{2}∠ABC+∠CPB),\therefore ∠CAB=2∠CPB$,故③正确.
∵$Rt△PMA\cong Rt△PQA,Rt△PQC\cong Rt△PNC,\therefore S_{△PAC}=S_{△MAP}+S_{△NCP}$,故④正确.综上,正确的个数为4.

10 如图,△ABC的三边AB,AC,BC的长分别为4,6,8,∠BAC,∠ABC,∠ACB的平分线将△ABC分成三个三角形,则$S_{△OAB}:S_{△OAC}:S_{△OBC}$= ______.


答案:
$2:3:4$ 如图,过点O分别作$OD⊥AB$于点D,$OE⊥AC$于点E,$OF⊥BC$于点F.
∵ O是$∠BAC,∠ABC,∠ACB$的平分线的交点,$\therefore OD=OE=OF.\because AB=4,AC=6,BC=8,\therefore S_{△OAB}:S_{△OAC}:S_{△OBC}=2:3:4.$

$2:3:4$ 如图,过点O分别作$OD⊥AB$于点D,$OE⊥AC$于点E,$OF⊥BC$于点F.
∵ O是$∠BAC,∠ABC,∠ACB$的平分线的交点,$\therefore OD=OE=OF.\because AB=4,AC=6,BC=8,\therefore S_{△OAB}:S_{△OAC}:S_{△OBC}=2:3:4.$

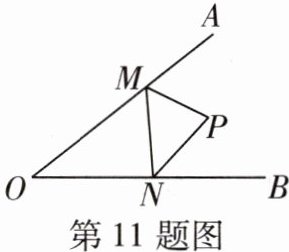
11 [2024无锡侨谊实验学校月考]如图,在∠AOB的边OA,OB上取点M,N,连接MN,MP平分∠AMN,NP平分∠MNB.若MN= 2,△PMN的面积是2,△OMN的面积是8,则OM+ON的长是______.

答案:
10 如图,过点P作$PE⊥OB$,垂足为E,过点P作$PF⊥MN$,垂足为F,过点P作$PG⊥OA$,垂足为G,连接OP.
∵ P是$△MON$外角平分线的交点,$\therefore PF=PG=PE.\because MN=2,△PMN$的面积是2,$\therefore \frac{1}{2}MN·PF=2,\therefore PF=2,\therefore PG=PE=2.\because △OMN$的面积是8,$\therefore △OMP$的面积+$△ONP$的面积$-△PMN$的面积$=8,\therefore \frac{1}{2}OM·PG+\frac{1}{2}ON·PE-2=8,\therefore OM+ON=10.$

10 如图,过点P作$PE⊥OB$,垂足为E,过点P作$PF⊥MN$,垂足为F,过点P作$PG⊥OA$,垂足为G,连接OP.
∵ P是$△MON$外角平分线的交点,$\therefore PF=PG=PE.\because MN=2,△PMN$的面积是2,$\therefore \frac{1}{2}MN·PF=2,\therefore PF=2,\therefore PG=PE=2.\because △OMN$的面积是8,$\therefore △OMP$的面积+$△ONP$的面积$-△PMN$的面积$=8,\therefore \frac{1}{2}OM·PG+\frac{1}{2}ON·PE-2=8,\therefore OM+ON=10.$

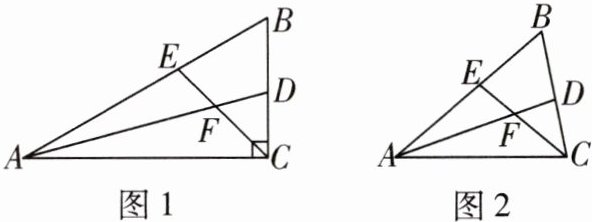
12 一题多解如图1,在Rt△ABC中,∠ACB= 90°,∠B= 60°,AD,CE分别是∠BAC,∠BCA的平分线,AD,CE相交于点F.
(1)请判断FE与FD之间的数量关系,并说明理由.
(2)如图2,如果∠ACB不是直角,其他条件不变,(1)中所得的结论是否仍然成立?请说明理由.
(1)请判断FE与FD之间的数量关系,并说明理由.
(2)如图2,如果∠ACB不是直角,其他条件不变,(1)中所得的结论是否仍然成立?请说明理由.

答案:
解:
(1)$FE=FD$.理由如下:
通解 过点F作$FM⊥AB$于点M,$FN⊥BC$于点N,则$∠FME=∠FND=90^{\circ }.\because CE$是$∠BCA$的平分线,$∠ACB=90^{\circ },∠B=60^{\circ },\therefore ∠BAC=90^{\circ }-∠B=30^{\circ },∠ACE=\frac{1}{2}∠ACB=45^{\circ }.\because AD$是$∠BAC$的平分线,$\therefore ∠BAD=\frac{1}{2}∠BAC=15^{\circ },\therefore ∠FEM=∠BAC+∠ACE=30^{\circ }+45^{\circ }=75^{\circ },∠FDN=∠B+∠BAD=60^{\circ }+15^{\circ }=75^{\circ },\therefore ∠FEM=∠FDN.\because ∠BAC,∠BCA$的平分线AD,CE交于点F,$\therefore$点F在$∠ABC$的平分线上.又$\because FM⊥AB,FN⊥BC,\therefore FM=FN,\therefore △FEM\cong △FDN,\therefore FE=FD.$
另解 过点F分别作$FM⊥AB$于点M,$FH⊥AC$于点H,$FN⊥BC$于点N,则$∠FME=∠FND=90^{\circ },\therefore ∠MFN=180^{\circ }-∠B=180^{\circ }-60^{\circ }=120^{\circ }.\because AD$平分$∠BAC$,CE平分$∠ACB,\therefore FM=FH=FN$,且$∠DAC=\frac{1}{2}∠BAC,∠ECA=\frac{1}{2}∠ACB.\because ∠B=60^{\circ },∠ACB=90^{\circ },\therefore ∠BAC=30^{\circ },∠ACE=45^{\circ },\therefore ∠DAC=15^{\circ },\therefore ∠DFE=∠AFC=180^{\circ }-15^{\circ }-45^{\circ }=120^{\circ },\therefore ∠MFN=∠DFE,\therefore ∠EFM=∠DFN,\therefore △FEM\cong △FDN,\therefore FE=FD.$
(2)成立.理由如下:过点F作$FM⊥AB$于点M,$FN⊥BC$于点N,则$FM=FN,∠FME=∠FND=90^{\circ }.\because ∠FDN=∠B+∠BAD=60^{\circ }+\frac{1}{2}∠BAC,∠FEM=∠BAC+∠ACE=∠BAC+\frac{1}{2}(180^{\circ }-∠B-∠BAC)=∠BAC+\frac{1}{2}(180^{\circ }-60^{\circ }-∠BAC)=60^{\circ }+\frac{1}{2}∠BAC,\therefore ∠FEM=∠FDN,\therefore △FEM\cong △FDN,\therefore FE=FD.$
(1)$FE=FD$.理由如下:
通解 过点F作$FM⊥AB$于点M,$FN⊥BC$于点N,则$∠FME=∠FND=90^{\circ }.\because CE$是$∠BCA$的平分线,$∠ACB=90^{\circ },∠B=60^{\circ },\therefore ∠BAC=90^{\circ }-∠B=30^{\circ },∠ACE=\frac{1}{2}∠ACB=45^{\circ }.\because AD$是$∠BAC$的平分线,$\therefore ∠BAD=\frac{1}{2}∠BAC=15^{\circ },\therefore ∠FEM=∠BAC+∠ACE=30^{\circ }+45^{\circ }=75^{\circ },∠FDN=∠B+∠BAD=60^{\circ }+15^{\circ }=75^{\circ },\therefore ∠FEM=∠FDN.\because ∠BAC,∠BCA$的平分线AD,CE交于点F,$\therefore$点F在$∠ABC$的平分线上.又$\because FM⊥AB,FN⊥BC,\therefore FM=FN,\therefore △FEM\cong △FDN,\therefore FE=FD.$
另解 过点F分别作$FM⊥AB$于点M,$FH⊥AC$于点H,$FN⊥BC$于点N,则$∠FME=∠FND=90^{\circ },\therefore ∠MFN=180^{\circ }-∠B=180^{\circ }-60^{\circ }=120^{\circ }.\because AD$平分$∠BAC$,CE平分$∠ACB,\therefore FM=FH=FN$,且$∠DAC=\frac{1}{2}∠BAC,∠ECA=\frac{1}{2}∠ACB.\because ∠B=60^{\circ },∠ACB=90^{\circ },\therefore ∠BAC=30^{\circ },∠ACE=45^{\circ },\therefore ∠DAC=15^{\circ },\therefore ∠DFE=∠AFC=180^{\circ }-15^{\circ }-45^{\circ }=120^{\circ },\therefore ∠MFN=∠DFE,\therefore ∠EFM=∠DFN,\therefore △FEM\cong △FDN,\therefore FE=FD.$
(2)成立.理由如下:过点F作$FM⊥AB$于点M,$FN⊥BC$于点N,则$FM=FN,∠FME=∠FND=90^{\circ }.\because ∠FDN=∠B+∠BAD=60^{\circ }+\frac{1}{2}∠BAC,∠FEM=∠BAC+∠ACE=∠BAC+\frac{1}{2}(180^{\circ }-∠B-∠BAC)=∠BAC+\frac{1}{2}(180^{\circ }-60^{\circ }-∠BAC)=60^{\circ }+\frac{1}{2}∠BAC,\therefore ∠FEM=∠FDN,\therefore △FEM\cong △FDN,\therefore FE=FD.$
13 教材习题变式已知∠AOB= 90°,OM是∠AOB的平分线,D是边OB上一点,将三角板的直角顶点P在射线OM上移动,使一直角边经过点D,另一直角边与边OA交于点C.
(1)如图1,求证:PC= PD.
(2)若另一直角边与边OA的反向延长线交于点C(如图2所示),则PC与PD还会相等吗?若相等,请予以证明;若不相等,请说明理由.
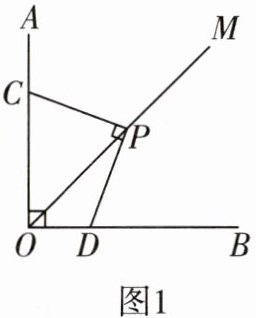

(1)如图1,求证:PC= PD.
(2)若另一直角边与边OA的反向延长线交于点C(如图2所示),则PC与PD还会相等吗?若相等,请予以证明;若不相等,请说明理由.


答案:
$(1)$ 证明$PC = PD$
解:过点$P$作$PE\perp OA$于点$E$,$PF\perp OB$于点$F$。
因为$OM$是$\angle AOB$的平分线,根据角平分线的性质:角平分线上的点到角两边的距离相等,所以$PE = PF$。
又因为$\angle AOB = 90^{\circ}$,$\angle CPD = 90^{\circ}$,所以$\angle CPE+\angle EPD=\angle DPF+\angle EPD = 90^{\circ}$,则$\angle CPE=\angle DPF$。
在$\triangle PCE$和$\triangle PDF$中:
$\begin{cases}\angle PEC=\angle PFD = 90^{\circ}\\PE = PF\\\angle CPE=\angle DPF\end{cases}$
根据“角 - 边 - 角”($ASA$)全等判定定理,可得$\triangle PCE\cong\triangle PDF$。
根据全等三角形的性质:全等三角形的对应边相等,所以$PC = PD$。
$(2)$ 判断$PC$与$PD$是否相等并证明
解:过点$P$作$PE\perp OA$于点$E$,$PF\perp OB$于点$F$。
因为$OM$是$\angle AOB$的平分线,所以$PE = PF$。
因为$\angle AOB = 90^{\circ}$,$\angle CPD = 90^{\circ}$,所以$\angle CPE+\angle EPD=\angle DPF+\angle EPD = 90^{\circ}$,则$\angle CPE=\angle DPF$。
在$\triangle PCE$和$\triangle PDF$中:
$\begin{cases}\angle PEC=\angle PFD = 90^{\circ}\\PE = PF\\\angle CPE=\angle DPF\end{cases}$
根据“角 - 边 - 角”($ASA$)全等判定定理,可得$\triangle PCE\cong\triangle PDF$。
根据全等三角形的性质,所以$PC = PD$。
综上,$(1)$ 可证得$PC = PD$;$(2)$ $PC$与$PD$相等 。

$(1)$ 证明$PC = PD$
解:过点$P$作$PE\perp OA$于点$E$,$PF\perp OB$于点$F$。
因为$OM$是$\angle AOB$的平分线,根据角平分线的性质:角平分线上的点到角两边的距离相等,所以$PE = PF$。
又因为$\angle AOB = 90^{\circ}$,$\angle CPD = 90^{\circ}$,所以$\angle CPE+\angle EPD=\angle DPF+\angle EPD = 90^{\circ}$,则$\angle CPE=\angle DPF$。
在$\triangle PCE$和$\triangle PDF$中:
$\begin{cases}\angle PEC=\angle PFD = 90^{\circ}\\PE = PF\\\angle CPE=\angle DPF\end{cases}$
根据“角 - 边 - 角”($ASA$)全等判定定理,可得$\triangle PCE\cong\triangle PDF$。
根据全等三角形的性质:全等三角形的对应边相等,所以$PC = PD$。
$(2)$ 判断$PC$与$PD$是否相等并证明
解:过点$P$作$PE\perp OA$于点$E$,$PF\perp OB$于点$F$。
因为$OM$是$\angle AOB$的平分线,所以$PE = PF$。
因为$\angle AOB = 90^{\circ}$,$\angle CPD = 90^{\circ}$,所以$\angle CPE+\angle EPD=\angle DPF+\angle EPD = 90^{\circ}$,则$\angle CPE=\angle DPF$。
在$\triangle PCE$和$\triangle PDF$中:
$\begin{cases}\angle PEC=\angle PFD = 90^{\circ}\\PE = PF\\\angle CPE=\angle DPF\end{cases}$
根据“角 - 边 - 角”($ASA$)全等判定定理,可得$\triangle PCE\cong\triangle PDF$。
根据全等三角形的性质,所以$PC = PD$。
综上,$(1)$ 可证得$PC = PD$;$(2)$ $PC$与$PD$相等 。

查看更多完整答案,请扫码查看


