第56页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
1 如图,a,b,c是数轴上三个点A,B,C所表示的实数。其中a是4的一个平方根,b是-27的立方根,c是1-3$\sqrt{2}$的相反数。
(1)填空:a=
(2)先化简,再求值:$\sqrt{c^{2}}$ + |a - b| - ($\sqrt[3]{a - c}$)^3。
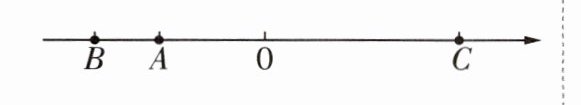
解:由题意可得,c>0,a - b>0,
∴$\sqrt{c^{2}}$ + |a - b| - ($\sqrt[3]{a - c}$)^3 = |c| + a - b - (a - c) = c + a - b - a + c = 2c - b。
∵b = -3,c = $3\sqrt{2} - 1$,
∴原式 = 2×($3\sqrt{2} - 1$) - (-3) = $6\sqrt{2} - 2 + 3$ = $6\sqrt{2} + 1$。
(1)填空:a=
-2
,b=-3
,c=$3\sqrt{2}-1$
;(2)先化简,再求值:$\sqrt{c^{2}}$ + |a - b| - ($\sqrt[3]{a - c}$)^3。
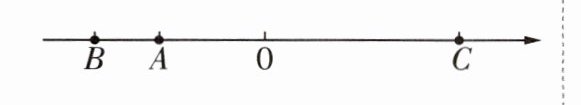
解:由题意可得,c>0,a - b>0,
∴$\sqrt{c^{2}}$ + |a - b| - ($\sqrt[3]{a - c}$)^3 = |c| + a - b - (a - c) = c + a - b - a + c = 2c - b。
∵b = -3,c = $3\sqrt{2} - 1$,
∴原式 = 2×($3\sqrt{2} - 1$) - (-3) = $6\sqrt{2} - 2 + 3$ = $6\sqrt{2} + 1$。
答案:
1解:
(1)-2 -3 $3\sqrt{2}-1$
(2)由题意可得,$c>0,a-b>0$,
$\therefore \sqrt{c^{2}}+|a-b|-\left(\sqrt[3]{a-c}\right)^{3}=|c|+a-b-(a-c)=c+a-b-a+c=2c-b$.
$\because b=-3,c=3\sqrt{2}-1$,
$\therefore$原式$=2×(3\sqrt{2}-1)-(-3)=6\sqrt{2}-2+3=6\sqrt{2}+1$.
(1)-2 -3 $3\sqrt{2}-1$
(2)由题意可得,$c>0,a-b>0$,
$\therefore \sqrt{c^{2}}+|a-b|-\left(\sqrt[3]{a-c}\right)^{3}=|c|+a-b-(a-c)=c+a-b-a+c=2c-b$.
$\because b=-3,c=3\sqrt{2}-1$,
$\therefore$原式$=2×(3\sqrt{2}-1)-(-3)=6\sqrt{2}-2+3=6\sqrt{2}+1$.
2 如图,一只蚂蚁从点A沿数轴向左爬了2个单位长度到达点B,点A表示的数为2-$\sqrt{2}$,设点B表示的数为m。
(1)实数m的值是
(2)在数轴上还有C,D两点分别表示c和d,若|2c + d|与$\sqrt{d^{2} - 25}$互为相反数,求2c - 3d的平方根。

解:$\because |2c+d|$与$\sqrt{d^{2}-25}$互为相反数,
$\therefore |2c+d|+\sqrt{d^{2}-25}=0$,
$\therefore |2c+d|=0,\sqrt{d^{2}-25}=0$,
解得$c=-\frac{5}{2},d=5$或$c=\frac{5}{2},d=-5$.
①当$c=-\frac{5}{2},d=5$时,
$2c-3d=-20$,无平方根;
②当$c=\frac{5}{2},d=-5$时,
$2c-3d=20$,
$\therefore 2c-3d$的平方根为$\pm \sqrt{20}$.
(1)实数m的值是
$-\sqrt{2}$
,|m + 1| + |m - 1|=$2\sqrt{2}$
;(2)在数轴上还有C,D两点分别表示c和d,若|2c + d|与$\sqrt{d^{2} - 25}$互为相反数,求2c - 3d的平方根。

解:$\because |2c+d|$与$\sqrt{d^{2}-25}$互为相反数,
$\therefore |2c+d|+\sqrt{d^{2}-25}=0$,
$\therefore |2c+d|=0,\sqrt{d^{2}-25}=0$,
解得$c=-\frac{5}{2},d=5$或$c=\frac{5}{2},d=-5$.
①当$c=-\frac{5}{2},d=5$时,
$2c-3d=-20$,无平方根;
②当$c=\frac{5}{2},d=-5$时,
$2c-3d=20$,
$\therefore 2c-3d$的平方根为$\pm \sqrt{20}$.
答案:
2解:
(1)$-\sqrt{2}$ $2\sqrt{2}$
$m=2-\sqrt{2}-2=-\sqrt{2}$.$\because m=-\sqrt{2}$,$\therefore m+1=1-\sqrt{2},m-1=-\sqrt{2}-1$,$\therefore |m+1|+|m-1|=\sqrt{2}-1+\sqrt{2}+1=2\sqrt{2}$.
(2)$\because |2c+d|$与$\sqrt{d^{2}-25}$互为相反数,
$\therefore |2c+d|+\sqrt{d^{2}-25}=0$,
$\therefore |2c+d|=0,\sqrt{d^{2}-25}=0$,
解得$c=-\frac{5}{2},d=5$或$c=\frac{5}{2},d=-5$.
①当$c=-\frac{5}{2},d=5$时,
$2c-3d=-20$,无平方根;
②当$c=\frac{5}{2},d=-5$时,
$2c-3d=20$,
$\therefore 2c-3d$的平方根为$\pm \sqrt{20}$.
(1)$-\sqrt{2}$ $2\sqrt{2}$
$m=2-\sqrt{2}-2=-\sqrt{2}$.$\because m=-\sqrt{2}$,$\therefore m+1=1-\sqrt{2},m-1=-\sqrt{2}-1$,$\therefore |m+1|+|m-1|=\sqrt{2}-1+\sqrt{2}+1=2\sqrt{2}$.
(2)$\because |2c+d|$与$\sqrt{d^{2}-25}$互为相反数,
$\therefore |2c+d|+\sqrt{d^{2}-25}=0$,
$\therefore |2c+d|=0,\sqrt{d^{2}-25}=0$,
解得$c=-\frac{5}{2},d=5$或$c=\frac{5}{2},d=-5$.
①当$c=-\frac{5}{2},d=5$时,
$2c-3d=-20$,无平方根;
②当$c=\frac{5}{2},d=-5$时,
$2c-3d=20$,
$\therefore 2c-3d$的平方根为$\pm \sqrt{20}$.
3 如图,网格中每个小正方形的边长为1,把图中阴影部分剪拼成一个正方形,正方形的边长为a。已知4 - a的整数部分和小数部分分别是x,y,求x - y的相反数。
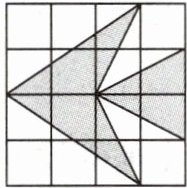

答案:
3解:$S_{阴影}=\frac{1}{2}×2×2×2+\frac{1}{2}×2×2=6$,$\therefore a^{2}=6$.
$\because a>0$,$\therefore a=\sqrt{6}$,$\therefore 4-a=4-\sqrt{6}$.
$\because \sqrt{4}<\sqrt{6}<\sqrt{9}$,$\therefore 2<\sqrt{6}<3$,$\therefore -3<-\sqrt{6}<-2$,$\therefore 1<4-\sqrt{6}<2$.
$\therefore x=1,y=4-\sqrt{6}-1=3-\sqrt{6}$,
$\therefore x-y=1-(3-\sqrt{6})=1-3+\sqrt{6}=-2+\sqrt{6}$,$\therefore x-y$的相反数为$-(-2+\sqrt{6})=2-\sqrt{6}$.
$\because a>0$,$\therefore a=\sqrt{6}$,$\therefore 4-a=4-\sqrt{6}$.
$\because \sqrt{4}<\sqrt{6}<\sqrt{9}$,$\therefore 2<\sqrt{6}<3$,$\therefore -3<-\sqrt{6}<-2$,$\therefore 1<4-\sqrt{6}<2$.
$\therefore x=1,y=4-\sqrt{6}-1=3-\sqrt{6}$,
$\therefore x-y=1-(3-\sqrt{6})=1-3+\sqrt{6}=-2+\sqrt{6}$,$\therefore x-y$的相反数为$-(-2+\sqrt{6})=2-\sqrt{6}$.
4 [2025福州十九中期中]小茗同学探索$\sqrt{145}$的近似值的过程如下:
∵面积为145的正方形的边长是$\sqrt{145}$,且12 < $\sqrt{145}$ < 13,
∴设$\sqrt{145}$ = 12 + x,其中0 < x < 1。
画出示意图,如图所示。

根据示意图,得图中正方形的面积为S_{正方形} = 12^2 + 2×12x + x^2。
依题意,得S_{正方形} = 145,
∴12^2 + 2×12x + x^2 = 145。
∵0 < x < 1,∴x^2 < 1,
此时可忽略x^2,得144 + 24x ≈ 145,解得x ≈ 0.04,
∴$\sqrt{145}$ ≈ 12.04,即$\sqrt{145}$的近似值是12.04。
(1)$\sqrt{270}$的整数部分为______。
(2)仿照小茗的探索过程,求$\sqrt{270}$的近似值。(画出示意图,标注数据,并写出求解过程,近似值精确到0.01)
∵面积为145的正方形的边长是$\sqrt{145}$,且12 < $\sqrt{145}$ < 13,
∴设$\sqrt{145}$ = 12 + x,其中0 < x < 1。
画出示意图,如图所示。

根据示意图,得图中正方形的面积为S_{正方形} = 12^2 + 2×12x + x^2。
依题意,得S_{正方形} = 145,
∴12^2 + 2×12x + x^2 = 145。
∵0 < x < 1,∴x^2 < 1,
此时可忽略x^2,得144 + 24x ≈ 145,解得x ≈ 0.04,
∴$\sqrt{145}$ ≈ 12.04,即$\sqrt{145}$的近似值是12.04。
(1)$\sqrt{270}$的整数部分为______。
(2)仿照小茗的探索过程,求$\sqrt{270}$的近似值。(画出示意图,标注数据,并写出求解过程,近似值精确到0.01)
答案:
4解:
(1)16
$\because 16^{2}=256,17^{2}=289$,$\therefore 16<\sqrt{270}<17$,$\therefore \sqrt{270}$的整数部分为16.
(2)$\because$面积为270的正方形的边长为$\sqrt{270}$,且$16<\sqrt{270}<17$,
$\therefore$设$\sqrt{270}=16+x$,其中$0<x<1$.
画出示意图,如图所示:

根据示意图,得图中正方形的面积为$S_{正方形}=16^{2}+2×16x+x^{2}$.
依题意,得$S_{正方形}=270$,
$\therefore 16^{2}+2×16x+x^{2}=270$.
$\because 0<x<1$,$\therefore x^{2}<1$,
此时可忽略$x^{2}$,得$256+32x\approx270$,解得$x\approx0.4375$,
$\therefore \sqrt{270}\approx16.4375$,
即$\sqrt{270}$的近似值是16.44.
4解:
(1)16
$\because 16^{2}=256,17^{2}=289$,$\therefore 16<\sqrt{270}<17$,$\therefore \sqrt{270}$的整数部分为16.
(2)$\because$面积为270的正方形的边长为$\sqrt{270}$,且$16<\sqrt{270}<17$,
$\therefore$设$\sqrt{270}=16+x$,其中$0<x<1$.
画出示意图,如图所示:

根据示意图,得图中正方形的面积为$S_{正方形}=16^{2}+2×16x+x^{2}$.
依题意,得$S_{正方形}=270$,
$\therefore 16^{2}+2×16x+x^{2}=270$.
$\because 0<x<1$,$\therefore x^{2}<1$,
此时可忽略$x^{2}$,得$256+32x\approx270$,解得$x\approx0.4375$,
$\therefore \sqrt{270}\approx16.4375$,
即$\sqrt{270}$的近似值是16.44.
查看更多完整答案,请扫码查看


