第61页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
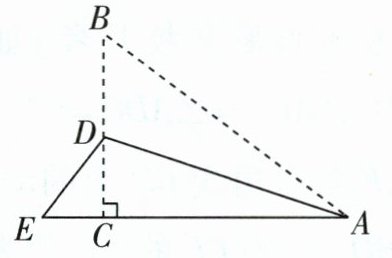
1 如图,有一张直角三角形纸片,$∠ACB= 90^{\circ },$$AC= 8cm,BC= 6cm$,将斜边 AB 翻折,使点 B落在直角边 AC 延长线上的点 E 处,折痕为AD,则 CE 的长为 (
A.1 cm
B.2 cm
C.3 cm
D.4 cm
B
)
A.1 cm
B.2 cm
C.3 cm
D.4 cm
答案:
B
∵在Rt△ACB中,∠ACB=90°,
∴AC²+BC²=AB²,
∴AB=10 cm.由折叠的性质,得AE=AB,
∴CE=AE-AC=AB-AC=2 cm.
∵在Rt△ACB中,∠ACB=90°,
∴AC²+BC²=AB²,
∴AB=10 cm.由折叠的性质,得AE=AB,
∴CE=AE-AC=AB-AC=2 cm.
2 如图,在$Rt△ABC$中,$∠B= 90^{\circ },AB= 6,BC= 9,$将$△ABC$折叠,使点 C 与 AB 的中点 D 重合,折痕交 AC 于点 M,交 BC 于点 N,则线段 BN 的长为 (
A.3
B.4
C.5
D.6
B
)A.3
B.4
C.5
D.6
答案:
B
∵D是AB的中点,AB=6,
∴AD=BD=3.由折叠的性质,得DN=CN,
∴BN=BC-CN=9-DN.在Rt△DBN中,DN²=BN²+DB²,
∴DN²=(9-DN)²+3²,
∴DN=5,
∴BN=4.
∵D是AB的中点,AB=6,
∴AD=BD=3.由折叠的性质,得DN=CN,
∴BN=BC-CN=9-DN.在Rt△DBN中,DN²=BN²+DB²,
∴DN²=(9-DN)²+3²,
∴DN=5,
∴BN=4.
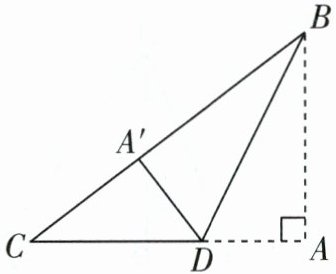
3 如图,在$Rt△ABC$中,$∠A= 90^{\circ },AB= 6,AC= 8.$现将$Rt△ABC$沿 BD 进行翻折,使点 A 落在BC 上的点$A'$处,则 CD 的长为 (
A.10
B.5
C.4
D.3
B
)
A.10
B.5
C.4
D.3
答案:
B
∵∠A=90°,AB=6,AC=8,
∴BC²=AB²+AC²=6²+8²=10²,
∴BC=10.由折叠的性质,得A'B=AB=6,∠BA'D=∠A=90°,A'D=AD,
∴A'C=BC-BA'=4.在Rt△A'CD中,由勾股定理,得CD²=A'D²+A'C²,
∴CD²=(8-CD)²+4²,
∴CD=5.
∵∠A=90°,AB=6,AC=8,
∴BC²=AB²+AC²=6²+8²=10²,
∴BC=10.由折叠的性质,得A'B=AB=6,∠BA'D=∠A=90°,A'D=AD,
∴A'C=BC-BA'=4.在Rt△A'CD中,由勾股定理,得CD²=A'D²+A'C²,
∴CD²=(8-CD)²+4²,
∴CD=5.
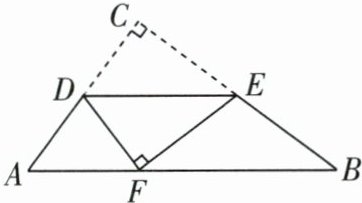
4 如图,在$△ABC$中,$∠C= 90^{\circ },AC= 6,BC= 8,$
点 D,E 分别在 AC,BC 上,且$DE// AB$.将
$△ABC$沿 DE 折叠,使点 C 落在斜边 AB 上的
点 F 处,则 AF 的长为 ( )
A.3.6
B.4
C.4.8
D.6.4
点 D,E 分别在 AC,BC 上,且$DE// AB$.将
$△ABC$沿 DE 折叠,使点 C 落在斜边 AB 上的
点 F 处,则 AF 的长为 ( )

A.3.6
B.4
C.4.8
D.6.4
答案:
A 如图,连接CF,根据题意,得CF⊥DE.因为DE//AB,
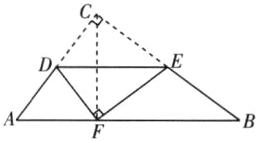
所以CF⊥AB.因为∠ACB=90°,AC=6,BC=8,所以AB²=AC²+BC²=10²,所以AB=10.因为AC⊥BC,CF⊥AB,所以$\frac{1}{2}AC\cdot BC=\frac{1}{2}AB\cdot CF$,所以CF=4.8,所以AF²=AC²-CF²=6²-4.8²=3.6²,所以AF=3.6.
A 如图,连接CF,根据题意,得CF⊥DE.因为DE//AB,

所以CF⊥AB.因为∠ACB=90°,AC=6,BC=8,所以AB²=AC²+BC²=10²,所以AB=10.因为AC⊥BC,CF⊥AB,所以$\frac{1}{2}AC\cdot BC=\frac{1}{2}AB\cdot CF$,所以CF=4.8,所以AF²=AC²-CF²=6²-4.8²=3.6²,所以AF=3.6.
5 如图,在三角形纸片 ABC 中,$∠BAC= 90^{\circ },$$AB= 2,AC= 3$,沿 AD 和 EF 将纸片折叠,使点B 和点 C 都落在边 BC 上的点 P 处,则 AE 的长是 (
A.$\frac {13}{6}$
B.$\frac {5}{6}$
C.$\frac {7}{6}$
D.$\frac {6}{5}$
A
)A.$\frac {13}{6}$
B.$\frac {5}{6}$
C.$\frac {7}{6}$
D.$\frac {6}{5}$
答案:
A
∵沿AD将纸片折叠,使点B落在边BC上的点P处,
∴AP=AB=2,∠B=∠APB.
∵沿EF将纸片折叠,使点C与点P重合,
∴CE=PE,∠C=∠EPF.
∵∠BAC=90°,
∴∠B+∠C=90°,
∴∠APB+∠EPF=90°,
∴∠APE=90°,
∴AP²+PE²=AE².设AE=x,则PE=CE=3-x,
∴2²+(3-x)²=x²,解得$x=\frac{13}{6}$,即$AE=\frac{13}{6}$.
∵沿AD将纸片折叠,使点B落在边BC上的点P处,
∴AP=AB=2,∠B=∠APB.
∵沿EF将纸片折叠,使点C与点P重合,
∴CE=PE,∠C=∠EPF.
∵∠BAC=90°,
∴∠B+∠C=90°,
∴∠APB+∠EPF=90°,
∴∠APE=90°,
∴AP²+PE²=AE².设AE=x,则PE=CE=3-x,
∴2²+(3-x)²=x²,解得$x=\frac{13}{6}$,即$AE=\frac{13}{6}$.
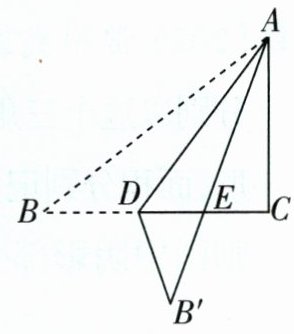
6 如图,在$Rt△ABC$中,$∠C= 90^{\circ },AC= 3,BC= 4,$
D 为 BC 上一点,将$△ABD$沿 AD 折叠至$△AB'D,$
$AB'$交线段 CD 于点 E. 当$△B'DE$是直角三角
形时,求点 D 到 AB 的距离.
D 为 BC 上一点,将$△ABD$沿 AD 折叠至$△AB'D,$
$AB'$交线段 CD 于点 E. 当$△B'DE$是直角三角
形时,求点 D 到 AB 的距离.

答案:
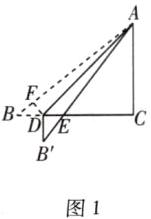
解:当点E不与点C重合时,此时∠B'DE=90°.如图1,过点D作DF⊥AB于点F.
∵∠C=90°,AC=3,BC=4,
∴$AB=\sqrt{AC^2+BC^2}=5$.由折叠的性质,得BD=B'D.
∵△B'DE是直角三角形,
∴∠BDB'=∠B'DE=90°.
∵∠ADB+∠BDB'+∠ADB'=360°,∠BDB'=90°,
∴∠ADB+∠ADB'=270°.由折叠的性质,得∠ADB=∠ADB',
∴∠ADB=∠ADB'=135°.
∴∠ADC=∠ADB'-∠B'DE=135°-90°=45°.又
∵∠C=90°,
∴△ADC是等腰直角三角形,
∴DC=AC=3,
∴BD=BC-DC=4-3=1.
∵$S_{\triangle ABD}=\frac{1}{2}AB\cdot DF=\frac{1}{2}BD\cdot AC$,
∴$DF=\frac{BD\cdot AC}{AB}=\frac{1×3}{5}=\frac{3}{5}$.
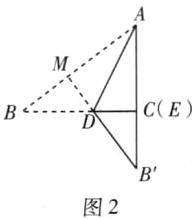
当点E与点C重合时,此时∠B'ED=90°.如图2,此时△B'DE是直角三角形.由折叠的性质,得∠BAD=∠CAD,即AD为∠BAC的平分线.过点D作DM⊥AB,垂足为M.
∵∠ACB=90°,
∴DC⊥AC,
∴DM=DC.由折叠的性质,得AB'=AB=5,BD=B'D.
∴B'C=AB'-AC=5-3=2.设CD=DM=x,则BD=B'D=4-x.
∵∠B'ED=90°,
∴B'D²=B'C²+CD²,
∴(4-x)²=2²+x²,解得$x=\frac{3}{2}$,即$DM=\frac{3}{2}$.
综上可知,点D到AB的距离为$\frac{3}{5}$或$\frac{3}{2}$.
解:当点E不与点C重合时,此时∠B'DE=90°.如图1,过点D作DF⊥AB于点F.
∵∠C=90°,AC=3,BC=4,
∴$AB=\sqrt{AC^2+BC^2}=5$.由折叠的性质,得BD=B'D.
∵△B'DE是直角三角形,
∴∠BDB'=∠B'DE=90°.
∵∠ADB+∠BDB'+∠ADB'=360°,∠BDB'=90°,
∴∠ADB+∠ADB'=270°.由折叠的性质,得∠ADB=∠ADB',
∴∠ADB=∠ADB'=135°.
∴∠ADC=∠ADB'-∠B'DE=135°-90°=45°.又
∵∠C=90°,
∴△ADC是等腰直角三角形,
∴DC=AC=3,
∴BD=BC-DC=4-3=1.
∵$S_{\triangle ABD}=\frac{1}{2}AB\cdot DF=\frac{1}{2}BD\cdot AC$,
∴$DF=\frac{BD\cdot AC}{AB}=\frac{1×3}{5}=\frac{3}{5}$.

当点E与点C重合时,此时∠B'ED=90°.如图2,此时△B'DE是直角三角形.由折叠的性质,得∠BAD=∠CAD,即AD为∠BAC的平分线.过点D作DM⊥AB,垂足为M.
∵∠ACB=90°,
∴DC⊥AC,
∴DM=DC.由折叠的性质,得AB'=AB=5,BD=B'D.
∴B'C=AB'-AC=5-3=2.设CD=DM=x,则BD=B'D=4-x.
∵∠B'ED=90°,
∴B'D²=B'C²+CD²,
∴(4-x)²=2²+x²,解得$x=\frac{3}{2}$,即$DM=\frac{3}{2}$.

综上可知,点D到AB的距离为$\frac{3}{5}$或$\frac{3}{2}$.
查看更多完整答案,请扫码查看


