第60页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
8[2024无锡梁溪区期末]如果直角三角形的两条边长分别为2和3,那么它的第三条边长为 (
A.4
B.√5
C.√13
D.√5或√13
√5或√13
)A.4
B.√5
C.√13
D.√5或√13
答案:
当3为斜边长时,由勾股定理,得第三条边长为√(3²-2²)=√5;当3为直角边长时,由勾股定理,得第三条边长为√(3²+2²)=√13.综上所述,第三条边长为√5或√13.
解题通法
运用勾股定理求直角三角形的边长的方法
运用勾股定理时,要先根据直角三角形中的直角确定所求边是直角边还是斜边,再借助勾股定理求解.若题目中既没有明确直角也没有明确斜边或直角边,则要分类讨论,必要时需画出草图.
解题通法
运用勾股定理求直角三角形的边长的方法
运用勾股定理时,要先根据直角三角形中的直角确定所求边是直角边还是斜边,再借助勾股定理求解.若题目中既没有明确直角也没有明确斜边或直角边,则要分类讨论,必要时需画出草图.
9[2024无锡宜兴月考]如图,在△ABC中,AB= 6,AC= 9,AD⊥BC于点D,M为AD上任意一点,则$MC^2-MB^2$等于 (
A.29
B.32
C.36
D.45
45
)A.29
B.32
C.36
D.45
答案:
∵AD⊥BC,
∴∠ADB=∠ADC=90°.在Rt△BDM和Rt△CDM中,MB²=BD²+MD²,MC²=CD²+MD².
∴MC² - MB²=(CD²+MD²)-(BD²+MD²)=CD² - BD².在Rt△ABD和Rt△ADC中,AB²=BD²+AD²,AC²=CD²+AD².
∴AC² - AB²=(CD²+AD²)-(BD²+AD²)=CD² - BD²,
∴MC² - MB²=AC² - AB²=9² - 6²=81 - 36=45.
∵AD⊥BC,
∴∠ADB=∠ADC=90°.在Rt△BDM和Rt△CDM中,MB²=BD²+MD²,MC²=CD²+MD².
∴MC² - MB²=(CD²+MD²)-(BD²+MD²)=CD² - BD².在Rt△ABD和Rt△ADC中,AB²=BD²+AD²,AC²=CD²+AD².
∴AC² - AB²=(CD²+AD²)-(BD²+AD²)=CD² - BD²,
∴MC² - MB²=AC² - AB²=9² - 6²=81 - 36=45.
10[2025常州武进区期中]如图,在Rt△ABC中,分别以这个三角形的三边为边长向外侧作正方形,面积分别记为$S_1,S_2,S_3.$若$S_3+S_2-S_1= 18,$则图中阴影部分的面积为______.
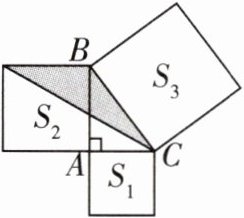

4.5
答案:
4.5 在Rt△ABC中,
∵∠BAC=90°,
∴AC²+AB²=BC²,
∴S₁+S₂=S₃.又
∵S₃+S₂ - S₁=18,
∴S₂=9,
∴阴影部分的面积=(1/2)S₂=(1/2)×9=4.5.
∵∠BAC=90°,
∴AC²+AB²=BC²,
∴S₁+S₂=S₃.又
∵S₃+S₂ - S₁=18,
∴S₂=9,
∴阴影部分的面积=(1/2)S₂=(1/2)×9=4.5.
11一题多解[2024无锡宜兴月考]如图,在△ABC中,∠C= 90°,AD平分∠BAC,AB= 10,AC= 6,则CD= ______.
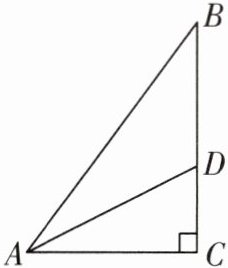

答案:
3 通解 如图,过点D作DE⊥AB于点E.在Rt△ABC中,由勾股定理,得BC=√(AB²-AC²)=√(10²-6²)=8.
∵AD平分∠BAC,AC⊥DC,DE⊥AB,
∴CD=DE.
∵S△ABC=S△ACD+S△ABD,
∴(1/2)AC·CD+(1/2)AB·DE=(1/2)AC·BC,
∴(1/2)×6CD+(1/2)×10CD=(1/2)×6×8,解得CD=3.
另解 如图,过点D作DE⊥AB于点E,则∠AED=∠DEB=∠C=90°.在Rt△ABC中,由勾股定理,得BC=√(AB²-AC²)=√(10²-6²)=8.
∵AD平分∠BAC,AC⊥DC,DE⊥AB,
∴CD=DE.在Rt△ADC和Rt△ADE中,{AD = AD, CD = ED},
∴Rt△ADC≌Rt△ADE(HL),
∴AE=AC=6.设CD=DE=x,则BD=BC - CD=8 - x,BE=AB - AE=10 - 6=4.
∵∠DEB=90°,
∴DE²+BE²=BD²,
∴x²+4²=(8 - x)²,解得x=3,即CD=3.

3 通解 如图,过点D作DE⊥AB于点E.在Rt△ABC中,由勾股定理,得BC=√(AB²-AC²)=√(10²-6²)=8.
∵AD平分∠BAC,AC⊥DC,DE⊥AB,
∴CD=DE.
∵S△ABC=S△ACD+S△ABD,
∴(1/2)AC·CD+(1/2)AB·DE=(1/2)AC·BC,
∴(1/2)×6CD+(1/2)×10CD=(1/2)×6×8,解得CD=3.
另解 如图,过点D作DE⊥AB于点E,则∠AED=∠DEB=∠C=90°.在Rt△ABC中,由勾股定理,得BC=√(AB²-AC²)=√(10²-6²)=8.
∵AD平分∠BAC,AC⊥DC,DE⊥AB,
∴CD=DE.在Rt△ADC和Rt△ADE中,{AD = AD, CD = ED},
∴Rt△ADC≌Rt△ADE(HL),
∴AE=AC=6.设CD=DE=x,则BD=BC - CD=8 - x,BE=AB - AE=10 - 6=4.
∵∠DEB=90°,
∴DE²+BE²=BD²,
∴x²+4²=(8 - x)²,解得x=3,即CD=3.

12[2024常州期中]如图,有一个面积为1的正方形,经过1次“生长”,它上边的两个顶点生出了两个小正方形,且三个正方形围成的三角形是直角三角形,再经过1次“生长”,变成了如图所示的图形.若“生长”2024次,则图中所有正方形的面积和为______.
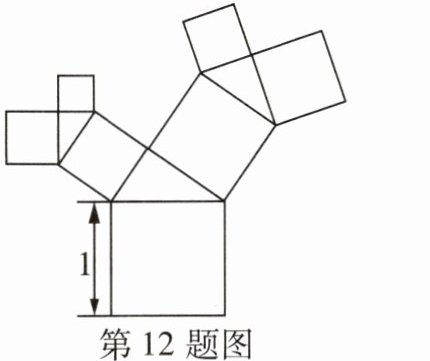

答案:
2025 如图,由题意,得正方形A的面积为1.由勾股定理,得正方形B的面积+正方形C的面积=1,
∴“生长”1次时图中所有正方形的面积和为2,同理可得,“生长”2次时图中所有正方形的面积和为3……
∴“生长”2024次时图中所有正方形的面积和为2025.

2025 如图,由题意,得正方形A的面积为1.由勾股定理,得正方形B的面积+正方形C的面积=1,
∴“生长”1次时图中所有正方形的面积和为2,同理可得,“生长”2次时图中所有正方形的面积和为3……
∴“生长”2024次时图中所有正方形的面积和为2025.

13[2025苏州景城学校月考]如图,在四边形ABCD中,∠ABC= ∠ADC= 90°,E是对角线AC的中点,F是对角线BD上的动点,连接EF.若AC= 8,BD= 6,则EF的最小值为______.
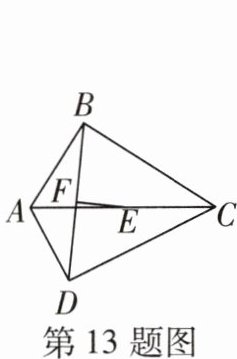

答案:
√7 如图,连接EB,ED,过点E作EF⊥BD于点F,此时EF的值最小.
∵在四边形ABCD中,∠ABC=∠ADC=90°,E是对角线AC的中点,
∴EB,ED分别是Rt△ABC和Rt△ADC的斜边上的中线,
∴EB=ED=(1/2)AC=(1/2)×8=4.又
∵EF⊥BD,
∴DF=BF=(1/2)BD=(1/2)×6=3,∠DFE=90°,
∴EF=√(DE² - DF²)=√(4² - 3²)=√7.

√7 如图,连接EB,ED,过点E作EF⊥BD于点F,此时EF的值最小.
∵在四边形ABCD中,∠ABC=∠ADC=90°,E是对角线AC的中点,
∴EB,ED分别是Rt△ABC和Rt△ADC的斜边上的中线,
∴EB=ED=(1/2)AC=(1/2)×8=4.又
∵EF⊥BD,
∴DF=BF=(1/2)BD=(1/2)×6=3,∠DFE=90°,
∴EF=√(DE² - DF²)=√(4² - 3²)=√7.

14推理能力[2024南京求真中学期中]如图,在△ABC中,AD⊥BC于点D,AB= 13,AD= 12,CD= 9,点P从点C出发,以每秒2个单位长度的速度沿着CD-DA运动,设点P运动的时间为t秒.
(1)当t的值为______时,AP平分△ABC的面积;
(2)求当t为何值时,△PAB为轴对称图形;
(3)若点E,F分别为AD,AB上的动点,则BE+EF的最小值为______.
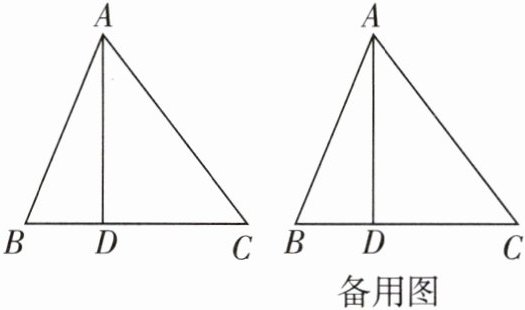
(1)当t的值为______时,AP平分△ABC的面积;
(2)求当t为何值时,△PAB为轴对称图形;
(3)若点E,F分别为AD,AB上的动点,则BE+EF的最小值为______.

答案:
解:
(1)7/2
∵AD⊥BC,
∴∠ADB=90°.
∵AD=12,AB=13,
∴BD²=AB² - AD²=25,
∴BD=5,
∴BC=DC+BD=14.
∵AP平分△ABC的面积,
∴点P为BC的中点,
∴CP=(1/2)BC=7,
∴t=7/2.
(2)由△PAB为轴对称图形,得△PAB是等腰三角形.
如图1,当BP=AB=13时,PC=BC - BP=14 - 13=1,
∴t=1/2.

如图2,当AP=AB=13时,点P只能在线段CD上.
∵AD⊥BC,
∴PD=BD=5,
∴BP=10,
∴PC=BC - BP=4,
∴t=4/2=2.

如图3,当BP=AP,且点P在线段CD上时,设DP=a,则AP=BP=5 + a.在Rt△ADP中,由勾股定理,得AP²=AD²+DP²,
∴(5 + a)²=12²+a²,解得a=119/10>9,即DP>DC,故此情况不成立.
如图4,当BP=AP,且点P在线段AD上时,过点P作PM⊥AB于点M.设PD=m,则BP=AP=12 - m.在Rt△BDP中,由勾股定理,得BP²=BD²+DP²,
∴(12 - m)²=5²+m²,解得m=119/24,
∴PD+CD=119/24+9=335/24,
∴t=335/48.
综上所述,当t的值为1/2或2或335/48时,△PAB为轴对称图形.



(3)120/13
如图5,在DC上取点G,使DG=BD,连接AG,过点G作GF⊥AB于点F,交AD于点E,此时BE+EF=GE+EF=GF,为最小值.由
(2)知BG=10.
∵S△ABG=(1/2)BG·AD=(1/2)AB·GF,
∴GF=(BG·AD)/AB=(10×12)/13=120/13,
∴BE+EF的最小值为120/13.
解:
(1)7/2
∵AD⊥BC,
∴∠ADB=90°.
∵AD=12,AB=13,
∴BD²=AB² - AD²=25,
∴BD=5,
∴BC=DC+BD=14.
∵AP平分△ABC的面积,
∴点P为BC的中点,
∴CP=(1/2)BC=7,
∴t=7/2.
(2)由△PAB为轴对称图形,得△PAB是等腰三角形.
如图1,当BP=AB=13时,PC=BC - BP=14 - 13=1,
∴t=1/2.

如图2,当AP=AB=13时,点P只能在线段CD上.
∵AD⊥BC,
∴PD=BD=5,
∴BP=10,
∴PC=BC - BP=4,
∴t=4/2=2.

如图3,当BP=AP,且点P在线段CD上时,设DP=a,则AP=BP=5 + a.在Rt△ADP中,由勾股定理,得AP²=AD²+DP²,
∴(5 + a)²=12²+a²,解得a=119/10>9,即DP>DC,故此情况不成立.
如图4,当BP=AP,且点P在线段AD上时,过点P作PM⊥AB于点M.设PD=m,则BP=AP=12 - m.在Rt△BDP中,由勾股定理,得BP²=BD²+DP²,
∴(12 - m)²=5²+m²,解得m=119/24,
∴PD+CD=119/24+9=335/24,
∴t=335/48.
综上所述,当t的值为1/2或2或335/48时,△PAB为轴对称图形.



(3)120/13
如图5,在DC上取点G,使DG=BD,连接AG,过点G作GF⊥AB于点F,交AD于点E,此时BE+EF=GE+EF=GF,为最小值.由
(2)知BG=10.
∵S△ABG=(1/2)BG·AD=(1/2)AB·GF,
∴GF=(BG·AD)/AB=(10×12)/13=120/13,
∴BE+EF的最小值为120/13.
查看更多完整答案,请扫码查看


