第6页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
1 如图,∠ABC,∠ACB的平分线相交于点O.
(1)当∠A= 50°时,求∠BOC的度数.
(2)当∠A= 90°时,求∠BOC的度数.
(3)当∠A= 120°时,求∠BOC的度数.
(4)从中你能发现∠BOC与∠A的数量关系吗?请直接写出.

(1)当∠A= 50°时,求∠BOC的度数.
(2)当∠A= 90°时,求∠BOC的度数.
(3)当∠A= 120°时,求∠BOC的度数.
(4)从中你能发现∠BOC与∠A的数量关系吗?请直接写出.

答案:
1 解:因为∠ABC,∠ACB的平分线相交于点O,所以∠OBC= $\frac{1}{2}$∠ABC,∠OCB= $\frac{1}{2}$∠ACB.在△OBC中,∠BOC=180°-∠OBC-∠OCB=180°- $\frac{1}{2}$(∠ABC+∠ACB).
(1)当∠A=50°时,∠ABC+∠ACB=130°,所以∠BOC=180°- $\frac{1}{2}$×130°=115°.
(2)当∠A=90°时,∠BOC=135°.
(3)当∠A=120°时,∠BOC=150°.
(4)能,∠BOC=90°+ $\frac{1}{2}$∠A.
名师点睛
解决本题的关键是灵活应用角平分线的定义,以及运用三角形内角和为180°来转换角.
(1)当∠A=50°时,∠ABC+∠ACB=130°,所以∠BOC=180°- $\frac{1}{2}$×130°=115°.
(2)当∠A=90°时,∠BOC=135°.
(3)当∠A=120°时,∠BOC=150°.
(4)能,∠BOC=90°+ $\frac{1}{2}$∠A.
名师点睛
解决本题的关键是灵活应用角平分线的定义,以及运用三角形内角和为180°来转换角.
2 已知AB⊥AC,D,E分别是射线AC,AB上的动点,∠AED的平分线与∠CDE的平分线所在直线相交于点M.
(1)如图1,已知∠ADE= 50°,求∠M的度数.
(2)如图2,当点D,E在射线AC,AB上运动时,∠M的大小是否发生变化?请说明理由.
(3)根据以上探究,请你指出关于三角形的角平分线的一条性质.

(1)如图1,已知∠ADE= 50°,求∠M的度数.
(2)如图2,当点D,E在射线AC,AB上运动时,∠M的大小是否发生变化?请说明理由.
(3)根据以上探究,请你指出关于三角形的角平分线的一条性质.

答案:
2 解:
(1)因为AB⊥AC,∠ADE=50°,所以∠CDE=130°,∠AED=40°.因为∠AED的平分线与∠CDE的平分线所在直线相交于点M,所以∠MED= $\frac{1}{2}$∠AED=20°,∠CDF= $\frac{1}{2}$∠CDE=65°,所以∠ADM=∠CDF=65°,所以∠M=180°-∠MED-∠ADM-∠ADE=45°.
(2)不变.理由如下:
如图,由
(1)可知∠AEM= $\frac{1}{2}$∠AED,
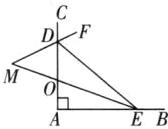
∠CDF= $\frac{1}{2}$∠CDE= $\frac{1}{2}$[180°-(180°-∠A-∠AED)]=∠ADM.因为∠A+∠AOE+∠AEM=∠M+∠ADM+∠DOM=180°,∠AOE=∠DOM,
三角形中角平分线的三种类型
所以∠A+ $\frac{1}{2}$∠AED=∠M+ $\frac{1}{2}$[180°-(180°-∠A-∠AED)],所以∠M= $\frac{1}{2}$∠A=45°.
(3)三角形的一个内角的平分线与另一个内角相邻外角的平分线的夹角等于第三个角的度数的一半.
2 解:
(1)因为AB⊥AC,∠ADE=50°,所以∠CDE=130°,∠AED=40°.因为∠AED的平分线与∠CDE的平分线所在直线相交于点M,所以∠MED= $\frac{1}{2}$∠AED=20°,∠CDF= $\frac{1}{2}$∠CDE=65°,所以∠ADM=∠CDF=65°,所以∠M=180°-∠MED-∠ADM-∠ADE=45°.
(2)不变.理由如下:
如图,由
(1)可知∠AEM= $\frac{1}{2}$∠AED,

∠CDF= $\frac{1}{2}$∠CDE= $\frac{1}{2}$[180°-(180°-∠A-∠AED)]=∠ADM.因为∠A+∠AOE+∠AEM=∠M+∠ADM+∠DOM=180°,∠AOE=∠DOM,
三角形中角平分线的三种类型
所以∠A+ $\frac{1}{2}$∠AED=∠M+ $\frac{1}{2}$[180°-(180°-∠A-∠AED)],所以∠M= $\frac{1}{2}$∠A=45°.
(3)三角形的一个内角的平分线与另一个内角相邻外角的平分线的夹角等于第三个角的度数的一半.
3 已知∠MON,点A,B分别在射线ON,OM上移动(不与点O重合),AD平分∠BAN,BC平分∠ABM,直线AD与BC交于点C.
(1)如图1,若∠MON= 90°,试猜想∠ACB的度数,并直接写出结果.
(2)如图2,若∠MON= α,问:点A,B在射线ON,OM上运动的过程中,∠ACB的度数是否改变?若不改变,求出其值(用含α的式子表示);若改变,请说明理由.
(3)如图3,若∠MON= α,BC平分∠ABO,其他条件不改变,问:点A,B在射线ON,OM上运动的过程中,∠ACB的度数是否改变?若不改变,求出其值(用含α的式子表示);若改变,请说明理由.

(1)如图1,若∠MON= 90°,试猜想∠ACB的度数,并直接写出结果.
(2)如图2,若∠MON= α,问:点A,B在射线ON,OM上运动的过程中,∠ACB的度数是否改变?若不改变,求出其值(用含α的式子表示);若改变,请说明理由.
(3)如图3,若∠MON= α,BC平分∠ABO,其他条件不改变,问:点A,B在射线ON,OM上运动的过程中,∠ACB的度数是否改变?若不改变,求出其值(用含α的式子表示);若改变,请说明理由.

答案:
3 解:
(1)∠ACB=45°.提示:因为AD平分∠BAN,BC平分∠ABM,所以∠NAD=∠BAD= $\frac{1}{2}$∠BAN,∠ABC=∠MBC= $\frac{1}{2}$∠ABM.因为∠BAO+∠ABO=180°-∠AOB=90°,所以∠CAB+∠CBA= $\frac{1}{2}$(∠BAN+∠ABM)= $\frac{1}{2}$×(360°-90°)=135°,所以∠ACB=180°-135°=45°.
(2)∠ACB的度数不改变.因为AD平分∠BAN,BC平分∠ABM,所以∠NAD=∠BAD= $\frac{1}{2}$∠BAN,∠ABC=∠MBC= $\frac{1}{2}$∠ABM.因为∠BAO+∠ABO=180°-∠AOB=180°-α,所以∠CAB+∠CBA= $\frac{1}{2}$(∠BAN+∠ABM)= $\frac{1}{2}$[360°-(180°-α)]=90°+ $\frac{1}{2}$α.所以∠ACB=180°-(∠CAB+∠CBA)=90°- $\frac{1}{2}$α.
(3)∠ACB的度数不改变.因为AD平分∠BAN,BC平分∠ABO,所以∠NAB=2∠BAD,∠OBA=2∠ABC.又因为∠NAB=180°-(180°-α-∠OBA)=α+∠OBA,所以2∠BAD=α+2∠ABC,所以∠BAD= $\frac{1}{2}$α+∠ABC,所以∠ACB=180°-∠CAB-∠ABC=180°-(180°-∠BAD)-∠ABC= $\frac{1}{2}$α.
(1)∠ACB=45°.提示:因为AD平分∠BAN,BC平分∠ABM,所以∠NAD=∠BAD= $\frac{1}{2}$∠BAN,∠ABC=∠MBC= $\frac{1}{2}$∠ABM.因为∠BAO+∠ABO=180°-∠AOB=90°,所以∠CAB+∠CBA= $\frac{1}{2}$(∠BAN+∠ABM)= $\frac{1}{2}$×(360°-90°)=135°,所以∠ACB=180°-135°=45°.
(2)∠ACB的度数不改变.因为AD平分∠BAN,BC平分∠ABM,所以∠NAD=∠BAD= $\frac{1}{2}$∠BAN,∠ABC=∠MBC= $\frac{1}{2}$∠ABM.因为∠BAO+∠ABO=180°-∠AOB=180°-α,所以∠CAB+∠CBA= $\frac{1}{2}$(∠BAN+∠ABM)= $\frac{1}{2}$[360°-(180°-α)]=90°+ $\frac{1}{2}$α.所以∠ACB=180°-(∠CAB+∠CBA)=90°- $\frac{1}{2}$α.
(3)∠ACB的度数不改变.因为AD平分∠BAN,BC平分∠ABO,所以∠NAB=2∠BAD,∠OBA=2∠ABC.又因为∠NAB=180°-(180°-α-∠OBA)=α+∠OBA,所以2∠BAD=α+2∠ABC,所以∠BAD= $\frac{1}{2}$α+∠ABC,所以∠ACB=180°-∠CAB-∠ABC=180°-(180°-∠BAD)-∠ABC= $\frac{1}{2}$α.
查看更多完整答案,请扫码查看


