第89页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
9 [2024 徐州中考]小明的速度与时间的函数关系如图所示,下列情境与之较为相符的是(
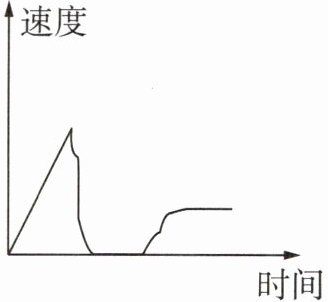
A.小明坐在门口,然后跑去看邻居家的小狗,随后坐着逗小狗玩
B.小明攀岩至高处,然后顺着杆子滑下来,随后躺在沙地上休息
C.小明跑去接电话,然后坐下来电话聊天,随后步行至另一个房间
D.小明步行去朋友家,敲门发现朋友不在家,随后步行回家
C
)
A.小明坐在门口,然后跑去看邻居家的小狗,随后坐着逗小狗玩
B.小明攀岩至高处,然后顺着杆子滑下来,随后躺在沙地上休息
C.小明跑去接电话,然后坐下来电话聊天,随后步行至另一个房间
D.小明步行去朋友家,敲门发现朋友不在家,随后步行回家
答案:
C
等腰三角形 $ ABC $ 的周长为 10 cm,底边 $ BC $ 的长为 $ y cm $,腰 $ AB $ 的长为 $ x cm $,则 $ y $ 与 $ x $ 之间的函数表达式为
y=-2x+10
,自变量 $ x $ 的取值范围是2.5<x<5
。
答案:
y=-2x+10 2.5<x<5
∵等腰三角形的两腰相等,周长为10 cm,
∴2x+y=10,
∴y与x之间的函数表达式为y=-2x+10.
∵x+x>y,y=-2x+10,
∴2x>-2x+10,解得x>2.5.
∵y>0,
∴-2x+10>0,解得x<5.
∴自变量x的取值范围是2.5<x<5.
∵等腰三角形的两腰相等,周长为10 cm,
∴2x+y=10,
∴y与x之间的函数表达式为y=-2x+10.
∵x+x>y,y=-2x+10,
∴2x>-2x+10,解得x>2.5.
∵y>0,
∴-2x+10>0,解得x<5.
∴自变量x的取值范围是2.5<x<5.
11 教材复习题变式 6 月 13 日,某港口的潮水高度 $ y(cm) $ 和时间 $ x(h) $ 的部分数据及函数图象如下:
| $ x/h $ | … | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | … |
| $ y/cm $ | … | 189 | 137 | 103 | 80 | 101 | 133 | 202 | 260 | … |
(数据来自某海洋研究所)

(1)数学活动:
①根据表中数据,通过描点、连线(光滑曲线)的方式补全该函数的图象.
②观察函数图象,当 $ x = 4 $ 时, $ y $ 的值为多少?当 $ y $ 的值最大时, $ x $ 的值为多少?
(2)数学思考:
请结合函数图象,写出该函数的两条性质或结论。
(3)数学应用:
根据研究,当潮水高度超过 260 cm 时,货轮能够安全进出该港口.问当天什么时间段适合货轮进出此港口?
| $ x/h $ | … | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | … |
| $ y/cm $ | … | 189 | 137 | 103 | 80 | 101 | 133 | 202 | 260 | … |
(数据来自某海洋研究所)

(1)数学活动:
①根据表中数据,通过描点、连线(光滑曲线)的方式补全该函数的图象.
②观察函数图象,当 $ x = 4 $ 时, $ y $ 的值为多少?当 $ y $ 的值最大时, $ x $ 的值为多少?
(2)数学思考:
请结合函数图象,写出该函数的两条性质或结论。
(3)数学应用:
根据研究,当潮水高度超过 260 cm 时,货轮能够安全进出该港口.问当天什么时间段适合货轮进出此港口?
答案:
(1)①补全的函数图象如图所示. ②观察函数图象,可知当x=4时,y=200;当y的值最大时,x=21.
②观察函数图象,可知当x=4时,y=200;当y的值最大时,x=21.
(2)答案不唯一.例如:当x=0和x=4时,y的值相等;当x=14时,y有最小值80.
(3)根据图象,当潮水高度超过260 cm时,5<x<10或18<x<23,即当天5时~10时或18时~23时适合货轮进出此港口.
(1)①补全的函数图象如图所示.
 ②观察函数图象,可知当x=4时,y=200;当y的值最大时,x=21.
②观察函数图象,可知当x=4时,y=200;当y的值最大时,x=21. (2)答案不唯一.例如:当x=0和x=4时,y的值相等;当x=14时,y有最小值80.
(3)根据图象,当潮水高度超过260 cm时,5<x<10或18<x<23,即当天5时~10时或18时~23时适合货轮进出此港口.
12 几何直观 [2024 宿迁崇文初级中学期末]如图 1,在长方形 $ ABCD $ 中, $ AB = 10 cm $, $ BC = 8 cm $.点 $ P $ 从点 $ A $ 出发,沿 $ A—B—C—D $ 路线运动,到点 $ D $ 停止,点 $ P $ 的速度为 $ 1 cm/s $, $ a s $ 时点 $ P $ 的速度变为 $ b cm/s $.图 2 是点 $ P $ 出发 $ x s $ 后, $ \triangle APD $ 的面积 $ S_{1}(cm^{2}) $ 与 $ x(s) $ 之间的函数关系图象。


(1)求 $ a $, $ b $ 及图 2 中 $ c $ 的值;
(2)设点 $ P $ 离开点 $ A $ 的路程为 $ y cm $,请求出动点 $ P $ 改变速度后 $ y(cm) $ 与出发后的运动时间 $ x(s) $ 之间的函数表达式。


(1)求 $ a $, $ b $ 及图 2 中 $ c $ 的值;
(2)设点 $ P $ 离开点 $ A $ 的路程为 $ y cm $,请求出动点 $ P $ 改变速度后 $ y(cm) $ 与出发后的运动时间 $ x(s) $ 之间的函数表达式。
答案:
(1)
∵在长方形ABCD中,AB=10 cm,BC=8 cm,
∴CD=AB=10 cm,AD=BC=8 cm.由题图2,a s时点P在线段AB上,此时AP=a cm,
∴$S_{\triangle APD}=\frac{1}{2}AD\cdot AP=\frac{1}{2}×8a=24$,解得a=6.由题图2知,8 s时点P与点B重合,则6+(8-6)b=10,解得b=2.由题图2知,8 s至c s,点P从点B运动到点D,速度为2 cm/s,则2(c-8)=8+10,解得c=17.
(2)
∵a=6,
∴6 s时点P的运动速度由1 cm/s变为2 cm/s,17 s时停止运动,6 s时点P离开点A的路程为1×6=6(cm),
∴y=2(x-6)+6=2x-6,
∴动点P改变速度后y(cm)与出发后的运动时间x(s)之间的函数表达式为y=2x-6(6<x≤17).
(1)
∵在长方形ABCD中,AB=10 cm,BC=8 cm,
∴CD=AB=10 cm,AD=BC=8 cm.由题图2,a s时点P在线段AB上,此时AP=a cm,
∴$S_{\triangle APD}=\frac{1}{2}AD\cdot AP=\frac{1}{2}×8a=24$,解得a=6.由题图2知,8 s时点P与点B重合,则6+(8-6)b=10,解得b=2.由题图2知,8 s至c s,点P从点B运动到点D,速度为2 cm/s,则2(c-8)=8+10,解得c=17.
(2)
∵a=6,
∴6 s时点P的运动速度由1 cm/s变为2 cm/s,17 s时停止运动,6 s时点P离开点A的路程为1×6=6(cm),
∴y=2(x-6)+6=2x-6,
∴动点P改变速度后y(cm)与出发后的运动时间x(s)之间的函数表达式为y=2x-6(6<x≤17).
查看更多完整答案,请扫码查看


