《2025年一遍过八年级数学上册苏科版》

1 如图,点 D,E 在△ABC 的边上,连接 AD,BE 交于点 F. 若 BD = CD,CE = $\frac{1}{3}AC$,$S_{△ABC}$ = 24,则 $S_{△AEF} - S_{△BDF}$ = (B)

答案： B 因为BD=CD,CE= $\frac{1}{3}$AC,$S_{\triangle ABC}=24$,所以$S_{\triangle ABE}=$ $\frac{2}{3}S_{\triangle ABC}=16$,$S_{\triangle ABD}=\frac{1}{2}S_{\triangle ABC}=12$,所以$S_{\triangle AEF}-S_{\triangle BDF}=$ $S_{\triangle ABE}-S_{\triangle ABD}=16-12=4$.

2 如图,在△ABC 中,D,E 分别是 BC,AD 的中点,点 F 在 BE 上,且 EF = 2BF. 若 $S_{△BCF}$ = 2,则 $S_{△ABC}$ = (D)

答案： D 因为EF=2BF,$S_{\triangle BCF}=2$,所以$S_{\triangle BEC}=3S_{\triangle BCF}=3× 2=6$.因为D是BC的中点,所以$S_{\triangle ABD}=S_{\triangle ACD}$,$S_{\triangle BDE}=S_{\triangle CDE}=$ $\frac{1}{2}S_{\triangle BEC}=3$.因为E是AD的中点,所以$S_{\triangle ABD}=S_{\triangle ACD}=$ $2S_{\triangle BDE}=6$,所以$S_{\triangle ABC}=2S_{\triangle ABD}=12$.

3 如图,AD 是△ABC 的中线,E 是 AD 的中点,连接 BE,CE. 若△ABC 的面积是 8,则阴影部分的面积为 (A)

答案： A 因为AD是△ABC的中线,所以$S_{\triangle ABD}=S_{\triangle ACD}=$ $\frac{1}{2}S_{\triangle ABC}$.因为E是AD的中点,所以$S_{\triangle ABE}=S_{\triangle BDE}=\frac{1}{2}S_{\triangle ABD}$,$S_{\triangle EDC}=S_{\triangle CAE}=\frac{1}{2}S_{\triangle ACD}$,所以$S_{\triangle ABE}=\frac{1}{4}S_{\triangle ABC}$,$S_{\triangle CDE}=\frac{1}{4}S_{\triangle ABC}$,所以$S_{阴影}=S_{\triangle ABE}+S_{\triangle CDE}=\frac{1}{4}S_{\triangle ABC}+\frac{1}{4}S_{\triangle ABC}=\frac{1}{2}S_{\triangle ABC}=\frac{1}{2}× 8=4$.

4 如图,△ABC 三边的中线 AD,BE,CF 的交点为 G. 若 $S_{△ABC}$ = 12,则图中阴影部分的面积是4.

答案： 4 设△AFG,△BFG,△BDG,△CDG,△CEG,△AEG的面积分别为$S_1,S_2,S_3,S_4,S_5,S_6$,根据中线平分三角形面积,得$S_1=S_2,S_3=S_4,S_5=S_6$,$S_1+S_2+S_3=S_4+S_5+S_6$①,$S_2+S_3+S_4=S_1+S_5+S_6$②,由①-②可得$S_1=S_4$,同理可得$S_2=S_5$,所以$S_1=S_2=S_3=S_4=S_5=S_6=2$,故阴影部分的面积为4.

1 如图,AD是△ABC的高,AE平分∠BAC.若∠B = 60°,∠C = 40°,则∠DAE的度数为10°.

答案： 10°
∵∠BAC+∠B+∠C=180°,∠B=60°,∠C=40°,
∴∠BAC=80°.
∵AE平分∠BAC,
∴∠BAE=∠CAE= $\frac{1}{2}$∠BAC=40°,
∴∠AEC=∠B+∠BAE=100°.
∵AD⊥BC,
∴∠ADE=90°,
∴∠DAE=∠AEC-∠ADE=10°.

2 如图,在△ABC中,AD是BC边上的高,AE平分∠BAC.已知∠B = 38°,∠CAD = 20°,则∠EAD = ______°.

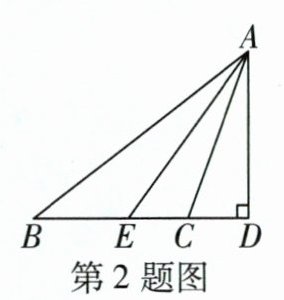
36

答案： 36
∵AD是BC边上的高,
∴∠D=90°.又
∵∠B=38°,
∴∠BAD=180°-∠B-∠D=180°-38°-90°=52°.
∵∠CAD=20°,
∴∠BAC=∠BAD-∠CAD=52°-20°=32°.
∵AE平分∠BAC,
∴∠EAC= $\frac{1}{2}$∠BAC=16°,
∴∠EAD=∠EAC+∠CAD=16°+20°=36°.

3 如图,D为△ABC的角平分线AE的延长线上的一点,过点D作DF⊥BC于点F.若∠B = 80°,∠C = 50°,则∠D的度数为______15°.

答案： 15° 在△ABC中,∠BAC=180°-∠B-∠C=180°-80°-50°=50°.
∵AD是∠BAC的平分线,
∴∠BAE= $\frac{1}{2}$∠BAC=25°.在△ABE中,∠AEB=180°-∠B-∠BAE=75°,
∴∠DEF=∠AEB=75°(对顶角相等).在△DEF中,DF⊥BC,
∴∠DFE=90°,
∴∠D=180°-∠DFE-∠DEF=180°-90°-75°=15°.

4 如图,AD平分∠BAC,点F在DA的延长线上,FE⊥BC于点E.若∠B = 40°,∠C = 70°,则∠DFE = 15°.

答案： 15
∵∠B=40°,∠C=70°,
∴∠BAC=180°-40°-70°=70°.
∵AD平分∠BAC,
∴∠BAD=∠CAD= $\frac{1}{2}$∠BAC=35°,
∴∠ADE=∠B+∠BAD=40°+35°=75°.
∵FE⊥BC,
∴∠FEB=90°,
∴∠DFE=180°-∠ADE-∠FEB=180°-75°-90°=15°.

5 如图,在△ABC中,AD是BC边上的高,AE,BF分别是∠BAC和∠ABC的平分线,它们相交于点O.若∠AOB = 130°,则∠CAD的度数为______.

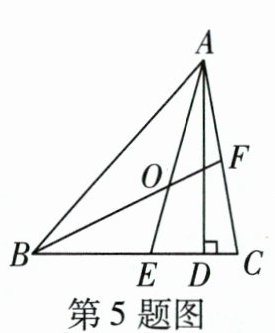
10°

答案： 10°
∵∠AOB=130°,
∴∠OAB+∠OBA=180°-130°=50°.
∵AE,BF分别是∠BAC和∠ABC的平分线,
∴∠BAC+∠ABC=2(∠OAB+∠OBA)=100°,
∴∠C=180°-100°=80°(三角形的内角和等于180°).
∵AD是BC边上高,
∴∠ADC=90°,
∴∠CAD=180°-90°-80°=10°.