第51页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
1 能够组成全体实数的是 (
A.自然数和负数
B.正数和负数
C.整数和分数
D.有理数和无理数
D
)A.自然数和负数
B.正数和负数
C.整数和分数
D.有理数和无理数
答案:
1 D 有理数和无理数统称为实数.实数分为正数、负数和0.
2 六个数:$0.123,\frac {15}{7},3.1416,-2π,(-1.5)^{3},$0.2020020002…(每相邻两个2之间依次多一个0).若其中无理数的个数为x,整数的个数为y,非负数的个数为z,则$x+y+z= $
6
.
答案:
2 6 无理数有$-2\pi$,0.202 002 000 2…(每相邻两个2之间依次多一个0),故$x=2$;没有整数,故$y=0$;非负数有0.123,$\frac{15}{7}$,3.141 6,0.202 002 000 2…(每相邻两个2之间依次多一个0),共4个,故$z=4$.故$x+y+z=6$.
3 教材练习变式[2024连云港月考]把下列各数填入相应的数集内.
-16,0.1515515551…(每相邻两个1之间依次多一个5),0,$-|-\frac {20}{3}|$,$|-1|$,$0.\dot {4}$,$-(-10)$,-5.6,$-\frac {π}{6}$.
正数集合:…{ };
无理数集合:…{ };
分数集合:…{ };
非负整数集合:…{ }.
-16,0.1515515551…(每相邻两个1之间依次多一个5),0,$-|-\frac {20}{3}|$,$|-1|$,$0.\dot {4}$,$-(-10)$,-5.6,$-\frac {π}{6}$.
正数集合:…{ };
无理数集合:…{ };
分数集合:…{ };
非负整数集合:…{ }.
答案:
3 解:正数集合:{0.151 551 555 1…(每相邻两个1之间依次多一个5),$|-1|$,$0.\dot{4}$,$-(-10)$,…};
无理数集合:{0.151 551 555 1…(每相邻两个1之间依次多一个5),$-\frac{\pi}{6}$,…};
分数集合:{$-|-\frac{20}{3}|$,$0.\dot{4}$,$-5.6$,…};
非负整数集合:{0,$|-1|$,$-(-10)$,…}.
无理数集合:{0.151 551 555 1…(每相邻两个1之间依次多一个5),$-\frac{\pi}{6}$,…};
分数集合:{$-|-\frac{20}{3}|$,$0.\dot{4}$,$-5.6$,…};
非负整数集合:{0,$|-1|$,$-(-10)$,…}.
4 给出下列结论:①数轴上的点只能表示无理数;②任何一个无理数都能用数轴上的点表示;③实数与数轴上的点一一对应;④有理数有无限个,无理数有有限个.
其中正确的是 (
A.①②
B.②③
C.③④
D.②③④
其中正确的是 (
B
)A.①②
B.②③
C.③④
D.②③④
答案:
4 B 数轴上的点既能表示无理数,也能表示有理数,故①错误;易知②③正确;有理数有无限个,无理数也有无限个,故④错误.
5 [2024南充中考]如图,数轴上表示$\sqrt {2}$的点是 (

A.点A
B.点B
C.点C
D.点D
C
)
A.点A
B.点B
C.点C
D.点D
答案:
5 C $\because 1<2<4$,$\therefore \sqrt{1}<\sqrt{2}<\sqrt{4}$,即$1<\sqrt{2}<2$.由数轴可知,只有点C表示的数在1和2之间.
6 [2025张家口期末]如图,在数轴上标注了四段范围,则表示$\sqrt {8}$的点落在 (
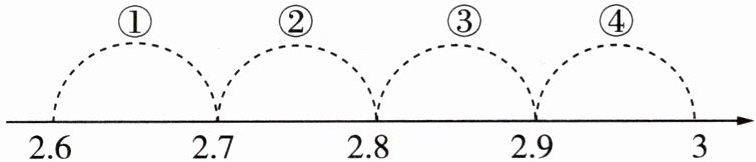
A.段①
B.段②
C.段③
D.段④
C
)
A.段①
B.段②
C.段③
D.段④
答案:
6 C $2.6^2=6.76$,$2.7^2=7.29$,$2.8^2=7.84$,$2.9^2=8.41$,$3^2=9$.$\because 7.84<8<8.41$,$\therefore 2.8<\sqrt{8}<2.9$,$\therefore$表示$\sqrt{8}$的点落在段③.
7 如图,面积为6的正方形ABCD的顶点A在数轴上,且表示的数为-1,若点E在数轴上(点E在点A的右侧),且$AB= AE$,则点E所表示的数为 (
A.$\sqrt {6}-1$
B.$\sqrt {6}$
C.$\sqrt {6}+1$
D.$\sqrt {6}+2$
A
)A.$\sqrt {6}-1$
B.$\sqrt {6}$
C.$\sqrt {6}+1$
D.$\sqrt {6}+2$
答案:
7 A $\because$正方形ABCD的面积为6,$\therefore AB^2=6$,$\therefore AB=\sqrt{6}$.$\because$点A表示的数是$-1$,$AE=AB$,$\therefore AE=\sqrt{6}$,$\therefore$点E表示的数是$\sqrt{6}-1$.
(1)数轴上点A表示的数为
(2)图中阴影部分的面积是多少?
(3)阴影正方形的边长是多少?在数轴上表示出点E,使点E表示的数为阴影正方形的边长.
-5
.(2)图中阴影部分的面积是多少?
解:∵正方形ABCD的面积为16,题图中阴影部分的面积为16-1/2×3×1×4=10.
(3)阴影正方形的边长是多少?在数轴上表示出点E,使点E表示的数为阴影正方形的边长.
解:∵题图中阴影部分的面积为10,∴阴影正方形的边长是√10,以原点为圆心,√10为半径画弧,与数轴正半轴交于点E,如图所示,点E即所求.
答案:
8 解:
(1)$-5$
$\because$正方形ABCD的面积为16,$\therefore AB=4$.$\because$数轴上点B表示的数为$-1$,由题图可知点A在点B左侧,$\therefore$点A表示的数为$-1-4=-5$.
(2)题图中阴影部分的面积为$16-\frac{1}{2}×3×1×4=10$.
(3)$\because$题图中阴影部分的面积为10,
$\therefore$阴影正方形的边长是$\sqrt{10}$,
以原点为圆心,$\sqrt{10}$为半径画弧,与数轴正半轴交于点E,如图所示,点E即所求.
(1)$-5$
$\because$正方形ABCD的面积为16,$\therefore AB=4$.$\because$数轴上点B表示的数为$-1$,由题图可知点A在点B左侧,$\therefore$点A表示的数为$-1-4=-5$.
(2)题图中阴影部分的面积为$16-\frac{1}{2}×3×1×4=10$.
(3)$\because$题图中阴影部分的面积为10,
$\therefore$阴影正方形的边长是$\sqrt{10}$,
以原点为圆心,$\sqrt{10}$为半径画弧,与数轴正半轴交于点E,如图所示,点E即所求.
查看更多完整答案,请扫码查看


