《2025年一遍过八年级数学上册苏科版》

1 [2025苏州高新区一中月考]如图,一艘轮船以12海里/时的速度从港口A出发向东北方向航行,另一艘轮船以5海里/时的速度同时从港口A出发向东南方向航行,离开港口2小时后两轮船相距( )


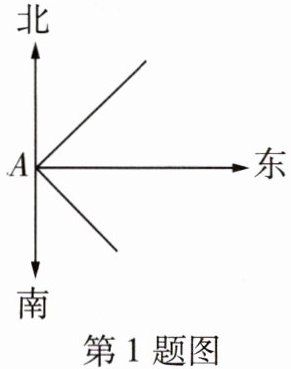
A.13海里
B.16海里
C.20海里
D.26海里

答案：
D 如图,
∵ 两轮船行驶的方向分别是东北方向和东南方向,
∴ ∠BAC=90°.2小时后,两艘轮船分别行驶了12×2=24(海里),5×2=10(海里).根据勾股定理,得2小时后两艘轮船之间的距离为√(24²+10²)=26(海里).

如图,将长为8cm的橡皮筋放置在水平面上,先固定两端A和B,然后把中点C垂直向上拉升3cm至点D,则橡皮筋被拉长了(2 cm)
A.2cm
B.3cm
C.4cm
D.6cm

答案： A 在Rt△ACD中,AC=1/2AB=4 cm,CD=3 cm.根据勾股定理,得AD²=AC²+DC²=25,所以AD=5 cm,所以AD+BD-AB=2AD-AB=10-8=2(cm).故橡皮筋被拉长了2 cm.

3 [跨学科·语文][2024吉林中考]图1中有一首古算诗,根据诗中的描述可以计算出红莲所在位置的湖水深度,其示意图如图2,其中AB= AB',AB⊥B'C于点C,BC= 0.5尺,B'C= 2尺.设AC的长度为x尺,可列方程为x²+2²=(x+0.5)².

答案： x²+2²=(x+0.5)² 在Rt△AB'C中,由勾股定理,得AC²+B'C²=AB'²,
∴ x²+2²=(x+0.5)².

4 [新趋势·数学文化][2025扬州江都区期末]如图,《九章算术》中有这样一道古题:今有一竖直着的木柱,在木柱的上端系有绳索,绳索从木柱的上端顺木柱下垂后堆在地面的部分有三尺(绳索比木柱长3尺),牵着绳索退行,在距木柱底部8尺(BC= 8尺)处时绳索用尽,则木柱长为55/6尺.

答案： 55/6 设木柱长为x尺.根据题意,得AB²+BC²=AC²,
∴ x²+8²=(x+3)²,解得x=55/6,即木柱长为55/6尺.

5 [2025盐城东台期末]图1是某品牌婴儿车,图2为其简化结构示意图.根据安全标准需满足BC⊥CD,现测得AB= CD= 6dm,BC= 3dm,AD= 9dm,其中AB与BD之间由一个固定为90°的零件连接(即∠ABD= 90°),通过计算说明该车是否符合安全标准.

答案： 解:在Rt△ABD中,BD²=AD²-AB²=9²-6²=45,在△BCD中,BC²+CD²=3²+6²=45,
∴ BC²+CD²=BD²,
∴ △BCD为直角三角形,且∠BCD=90°,
∴ BC⊥CD.故该车符合安全标准.

6 [跨学科·物理][2024连云港期末]小丽在物理实验课上利用如图所示的“光的反射演示器”直观呈现了光的反射原理.她用激光笔从量角器左边边缘点A处发出光线,经量角器圆心O处(此处放置平面镜)反射后,反射光线落在右边光屏CE上的点D处(C也在量角器的边缘上,O为量角器的中心,C,O,B三点共线,AB⊥BC,CE⊥BC).小丽在实验中还记录下了AB= 6cm,BC= 12cm.依据记录的数据,求量角器的半径OC的长.

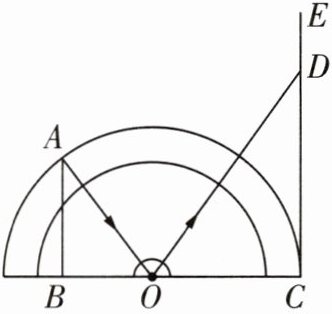
答案： 解:
∵ AB⊥BC,
∴ ∠ABC=90°.设OA=OC=x cm.
∵ BC=12 cm,
∴ BO=BC-OC=(12-x)cm.在Rt△ABO中,AB=6 cm,AB²+OB²=OA²,
∴ 6²+(12-x)²=x²,解得x=7.5,
∴ OA=OC=7.5 cm,
∴ 量角器的半径OC的长为7.5 cm.