《2025年一遍过八年级数学上册苏科版》

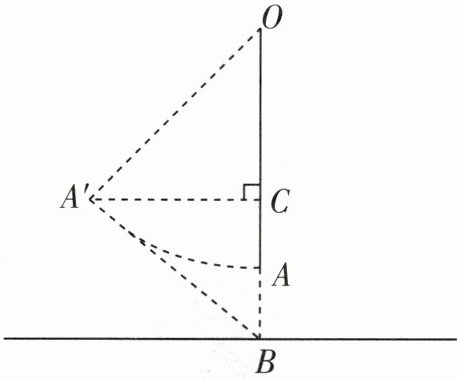
7 [2024南京玄武区期末]如图,当秋千OA静止时,最低点A离地面的距离AB为0.7m,当秋千摆动到OA'位置时,点A'与点B的距离A'B为2.5m,点A'水平移动的距离A'C为2m,求秋千OA的长.

答案： 解:由题意,得∠A'CO=∠A'CB=90°,
∴ BC²=A'B²-A'C²=2.25,
∴ BC=1.5 m,
∴ AC=BC-AB=1.5-0.7=0.8(m).设OA=OA'=x m,则OC=(x-0.8)m.在Rt△A'OC中,由勾股定理,得(x-0.8)²+2²=x²,解得x=2.9.故秋千OA的长为2.9 m.

如图,一支铅笔放在圆柱体笔筒中,笔筒的内部底面直径是9cm,内壁高12cm,则这支铅笔在笔筒内部的长度l的取值范围是(A)
A.12cm≤l≤15cm
B.9cm≤l≤12cm
C.10cm≤l≤15cm
D.10cm≤l≤12cm

答案： A 当铅笔不垂直于底面放置时,由勾股定理,得√(12²+9²)=15(cm).当铅笔垂直于笔筒底面放置时,铅笔在笔筒内部的长度为12 cm.所以这支铅笔在笔筒内部的长度l的取值范围是12 cm≤l≤15 cm.

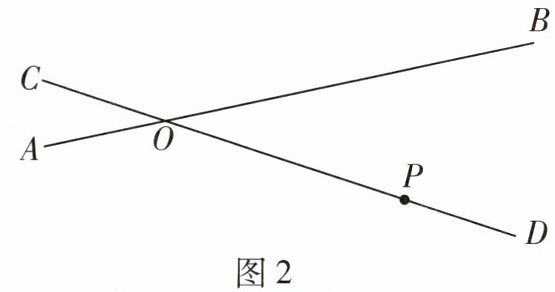
9 如图,铁路AB和公路CD在点O处相交,∠BOD= 30°,公路CD上的P距离点O处240m.如果火车行驶时,周围200m以内会受到噪音的影响,当火车在铁路AB上沿由A到B的方向以72km/h的速度行驶时,点P处受噪音影响的时间为( )

A.20s
B.16s
C.15s
D.25s

答案：
B 如图,过点P作PH⊥AB于点H,点E,F在AB上,且PE=PF=200 m.
∵ ∠BOD=30°,OP=240 m,
∴ PH=1/2OP=1/2×240=120(m).
∵ 火车行驶时,周围200 m以内会受到噪音的影响,
∴ 当火车行驶在E,F之间时,点P处会受到噪音的影响,
∴ EH=√(PE²-PH²)=√(200²-120²)=160(m).
∵ PE=PF,PH⊥EF,
∴ HF=HE=160 m,
∴ EF=320 m.
∵ 火车在铁路AB上沿由A到B的方向以72 km/h的速度行驶,72 km/h=20 m/s,
∴ 点P处受噪音影响的时间为320÷20=16(s).

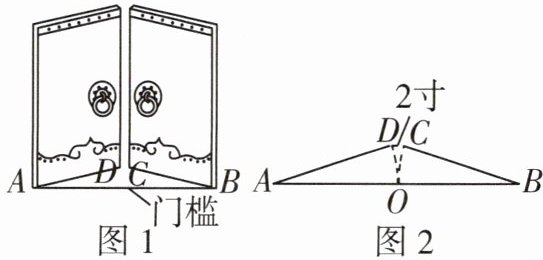
10 [新趋势·数学文化][2025连云港海州区期中]《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几何?题目大意:如图1和图2(图2为图1的平面示意图),推开双门,双门间隙CD的距离为2寸,点C和点D与门槛AB的距离都为1尺(1尺= 10寸),则AB的长是______寸.

答案：
101 过点D作DE⊥AB于点E,如图,由题意,得OA=OB=AD=BC,DE=1尺=10寸,OE=1/2CD=1寸.设OA=AD=r寸,则AB=2r寸,AE=(r-1)寸.在Rt△ADE中,AE²+DE²=AD²,即(r-1)²+10²=r²,解得r=50.5,所以AB=2r=101寸.

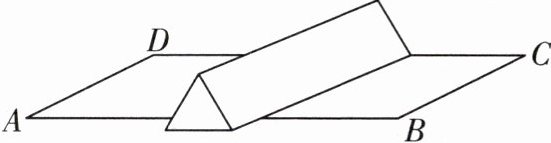
11 在一张长为11cm,宽为5cm的长方形纸片上,放置一个正三棱柱的纸盒(如图),它的侧棱平行且大于纸片的宽AD,它的底面是边长为1cm的等边三角形.一只蚂蚁从点A处爬到点C处的最短路程是______cm.

答案：
13 将纸盒在长方形纸片上展开后如图所示.由两点之间线段最短,知蚂蚁从点A处爬到点C处的最短路程为线段AC的长.由题意,得AB=11-1+2=12(cm),BC=5 cm,由勾股定理,得AC=√(AB²+BC²)=13 cm.即最短路程是13 cm.

12 [应用意识][2025无锡新吴区期中]盼盼家新装修了房子,如图是其中的三个房间甲、乙、丙,她将一个梯子斜靠在墙上,梯子顶端距离地面的垂直距离记作MA,如果梯子的底端P不动,顶端靠在对面墙上,此时梯子的顶端距离地面的垂直距离记作NB.
(1)当盼盼在甲房间时,梯子靠在对面墙上,顶端刚好落在对面墙角B处.若MA= 1.6米,AP= 1.2米,则甲房间的宽度AB= ______米.
(2)当她在乙房间时,测得MA= 2.4米,MP= 2.5米,且∠MPN= 90°,求乙房间的宽度AB.
(3)当她在丙房间时,测得MA= 2.8米,且∠MPA= 75°,∠NPB= 45°.
①求∠MPN的度数;
②求丙房间的宽度AB.

答案：
解:
(1)3.2 在Rt△AMP中,
∵ ∠A=90°,MA=1.6米,AP=1.2米,
∴ PM²=AM²+AP²=4,
∴ PM=2米.
∵ PB=PM=2米,
∴ 甲房间的宽度AB=AP+PB=3.2米.
(2)
∵ ∠MPN=90°,
∴ ∠APM+∠BPN=90°.又
∵ ∠APM+∠AMP=90°,
∴ ∠AMP=∠BPN.在△AMP和△BPN中,∠AMP=∠BPN,∠MAP=∠PBN=90°,MP=PN,
∴ △AMP≌△BPN(AAS),
∴ MA=PB=2.4米.
∵ PA²=PM²-AM²=0.49,
∴ PA=0.7米,
∴ AB=PA+PB=0.7+2.4=3.1(米).
∴ 乙房间的宽度AB是3.1米.
(3)①∠MPN=180°-∠APM-∠BPN=60°.②如图,过点N作MA的垂线,垂足为D,连接NM.
∵ DN//AB,
∴ ∠DNP=∠BPN=45°.
∵ ∠MPN=60°,PM=PN,
∴ △PNM为等边三角形,
∴ ∠PNM=60°,NM=PM,
∴ ∠MND=15°.
∵ ∠APM=75°,
∴ ∠AMP=15°,
∴ ∠DNM=∠AMP.在△AMP和△DNM中,∠AMP=∠DNM,∠MAP=∠NDM=90°,PM=MN,
∴ △AMP≌△DNM(AAS),
∴ AM=DN,
∴ AB=DN=AM=2.8米,即丙房间的宽度AB是2.8米.