第41页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
8 [2024威海中考]感悟
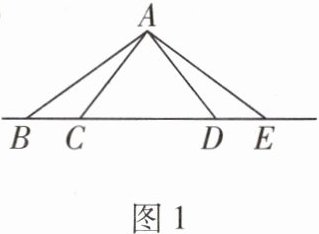
如图1,在△ABE中,点C,D在边BE上,AB= AE,BC= DE.求证:∠BAC= ∠EAD.
应用
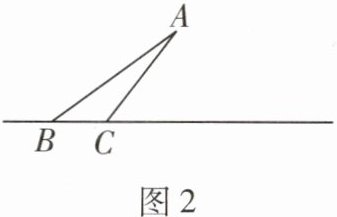
(1)如图2,用直尺和圆规在直线BC上取点D、点E(点D在点E的左侧),使得∠EAD= ∠BAC,且DE= BC(不写作法,保留作图痕迹);
(2)如图3,用直尺和圆规在直线AC上取一点D,在直线BC上取一点E,使得∠CDE= ∠BAC,且DE= AB(不写作法,保留作图痕迹).

如图1,在△ABE中,点C,D在边BE上,AB= AE,BC= DE.求证:∠BAC= ∠EAD.

应用
(1)如图2,用直尺和圆规在直线BC上取点D、点E(点D在点E的左侧),使得∠EAD= ∠BAC,且DE= BC(不写作法,保留作图痕迹);

(2)如图3,用直尺和圆规在直线AC上取一点D,在直线BC上取一点E,使得∠CDE= ∠BAC,且DE= AB(不写作法,保留作图痕迹).

答案:
8 感悟 证明:
∵AB=AE,
∴∠B=∠E.
在△ABC和△AED中,{AB=AE,∠B=∠E,BC=ED,
∴△ABC≌△AED,
∴∠BAC=∠EAD.
应用 解:
(1)解题思路:以点A为圆心,AB的长为半径画弧,交直线BC于一点,该点为点E,以点A为圆心,AC的长为半径画弧,交直线BC于一点,该点为点D,连接AD,AE.
如图1所示.

(2)解题思路:以点C为圆心,AC的长为半径画弧,交AC的延长线于一点,该点为点D,以点C为圆心,BC的长为半径画弧,交直线BC于一点,该点为点E,连接DE.
如图2所示.

8 感悟 证明:
∵AB=AE,
∴∠B=∠E.
在△ABC和△AED中,{AB=AE,∠B=∠E,BC=ED,
∴△ABC≌△AED,
∴∠BAC=∠EAD.
应用 解:
(1)解题思路:以点A为圆心,AB的长为半径画弧,交直线BC于一点,该点为点E,以点A为圆心,AC的长为半径画弧,交直线BC于一点,该点为点D,连接AD,AE.
如图1所示.

(2)解题思路:以点C为圆心,AC的长为半径画弧,交AC的延长线于一点,该点为点D,以点C为圆心,BC的长为半径画弧,交直线BC于一点,该点为点E,连接DE.
如图2所示.

9 [2024牡丹江中考节选]数学老师在课堂上给出了一个问题,让同学们探究.在Rt△ABC中,∠ACB= 90°,∠BAC= 30°,点D在直线BC上,将线段AD绕点A顺时针旋转60°得到线段AE,过点E作EF//BC,交直线AB于点F.

(1)当点D在线段BC上时,如图1,求证:BD+EF= AB.
分析问题:某同学在思考这道题时,想利用AD= AE构造全等三角形,便尝试着在AB上截取AM= EF,连接DM,通过证明两个三角形全等,最终证出结论.
推理证明:写出图1的证明过程.
探究问题
(2)当点D在线段BC的延长线上时,如图2;当点D在线段CB的延长线上时,如图3.请直接写出线段BD,EF,AB之间的数量关系.

(1)当点D在线段BC上时,如图1,求证:BD+EF= AB.
分析问题:某同学在思考这道题时,想利用AD= AE构造全等三角形,便尝试着在AB上截取AM= EF,连接DM,通过证明两个三角形全等,最终证出结论.
推理证明:写出图1的证明过程.
探究问题
(2)当点D在线段BC的延长线上时,如图2;当点D在线段CB的延长线上时,如图3.请直接写出线段BD,EF,AB之间的数量关系.
答案:
9
(1)证明:在AB上截取AM=EF,连接DM.
在Rt△ABC中,∠B=90° - ∠BAC=90° - 30°=60°.
∵EF//BC,
∴∠EFB=∠B=60°.
又
∵∠EAD=60°,
∴∠EFB=∠EAD.
又
∵∠BAD=∠EAD - ∠EAF,∠AEF=∠EFB - ∠EAF,
∴∠BAD=∠AEF.
又
∵AD=AE,AM=EF,
∴△DAM≌△AEF(SAS),
∴DM=AF,∠AMD=∠EFA=180° - ∠EFB=180° - 60°=120°,
∴∠BMD=180° - ∠AMD=180° - 120°=60°.
又
∵∠B=60°,
∴∠BMD=∠B=∠BDM,
∴△BMD是等边三角形,
∴BD=BM=DM.
∵BM + AM=AB,
∴BD + EF=AB.
(2)解:当点D在线段BC的延长线上时,AB=BD - EF;
当点D在线段CB的延长线上时,AB=EF - BD.
解法提示:如图1,当点D在线段BC的延长线上时,在BD上取点H,使BH=AB,连接AH并延长至点G,使AG=AF,连接DG.

∵∠ABC=60°,
∴△ABH是等边三角形,
∴∠BAH=60°.
∵线段AD绕点A顺时针旋转60°得到线段AE,
∴∠DAE=60°,AE=AD,
∴∠BAH=∠DAE,
∴∠BAH - ∠EAH=∠DAE - ∠EAH,即∠BAE=∠HAD,
又
∵AF=AG,
∴△FAE≌△GAD(SAS),
∴EF=DG,∠AFE=∠G.
∵BD//EF,
∴∠ABC=∠F=∠G=60°.
∵∠DHG=∠AHB=60°,
∴△DHG是等边三角形,
∴DH=DG=EF,
∴AB=BH=BD - DH=BD - EF.
如图2,当点D在线段CB的延长线上时,在EF上取点H,使AH=AF.

∵EF//BC,
∴∠F=∠ABC=60°.
∵AH=AF,
∴△AHF是等边三角形.
∴AH=FH,∠AHF=∠HAF=60°,
∴∠AHE=120°.
∵将线段AD绕点A顺时针旋转60°得到线段AE,
∴AD=AE,∠DAE=60°,
∴∠DAB + ∠EAH=180° - ∠EAD - ∠HAF=60°.
∵∠D + ∠DAB=∠ABC=60°,
∴∠D=∠EAH.
又
∵∠DBA=180° - ∠ABC=120°=∠EHA,AD=AE,
∴△ADB≌△EAH(AAS),
∴BD=AH,AB=EH.
∵AH=FH,
∴BD=FH,
∴AB=EH=EF - FH=EF - BD.
9
(1)证明:在AB上截取AM=EF,连接DM.
在Rt△ABC中,∠B=90° - ∠BAC=90° - 30°=60°.
∵EF//BC,
∴∠EFB=∠B=60°.
又
∵∠EAD=60°,
∴∠EFB=∠EAD.
又
∵∠BAD=∠EAD - ∠EAF,∠AEF=∠EFB - ∠EAF,
∴∠BAD=∠AEF.
又
∵AD=AE,AM=EF,
∴△DAM≌△AEF(SAS),
∴DM=AF,∠AMD=∠EFA=180° - ∠EFB=180° - 60°=120°,
∴∠BMD=180° - ∠AMD=180° - 120°=60°.
又
∵∠B=60°,
∴∠BMD=∠B=∠BDM,
∴△BMD是等边三角形,
∴BD=BM=DM.
∵BM + AM=AB,
∴BD + EF=AB.
(2)解:当点D在线段BC的延长线上时,AB=BD - EF;
当点D在线段CB的延长线上时,AB=EF - BD.
解法提示:如图1,当点D在线段BC的延长线上时,在BD上取点H,使BH=AB,连接AH并延长至点G,使AG=AF,连接DG.

∵∠ABC=60°,
∴△ABH是等边三角形,
∴∠BAH=60°.
∵线段AD绕点A顺时针旋转60°得到线段AE,
∴∠DAE=60°,AE=AD,
∴∠BAH=∠DAE,
∴∠BAH - ∠EAH=∠DAE - ∠EAH,即∠BAE=∠HAD,
又
∵AF=AG,
∴△FAE≌△GAD(SAS),
∴EF=DG,∠AFE=∠G.
∵BD//EF,
∴∠ABC=∠F=∠G=60°.
∵∠DHG=∠AHB=60°,
∴△DHG是等边三角形,
∴DH=DG=EF,
∴AB=BH=BD - DH=BD - EF.
如图2,当点D在线段CB的延长线上时,在EF上取点H,使AH=AF.

∵EF//BC,
∴∠F=∠ABC=60°.
∵AH=AF,
∴△AHF是等边三角形.
∴AH=FH,∠AHF=∠HAF=60°,
∴∠AHE=120°.
∵将线段AD绕点A顺时针旋转60°得到线段AE,
∴AD=AE,∠DAE=60°,
∴∠DAB + ∠EAH=180° - ∠EAD - ∠HAF=60°.
∵∠D + ∠DAB=∠ABC=60°,
∴∠D=∠EAH.
又
∵∠DBA=180° - ∠ABC=120°=∠EHA,AD=AE,
∴△ADB≌△EAH(AAS),
∴BD=AH,AB=EH.
∵AH=FH,
∴BD=FH,
∴AB=EH=EF - FH=EF - BD.
查看更多完整答案,请扫码查看


