《2025年一遍过八年级数学上册苏科版》

1 已知一个函数的变量 y 与自变量 x 的几组对应值如表,则这个函数的表达式可以是(A)
|x|…|-1|0|1|2|…|
|y|…|-2|0|2|4|…|
A.$ y = 2x $
B.$ y = x - 1 $
C.$ y = \frac{2}{x} $
D.$ y = x^{2} $

答案： A 根据表中数据可以看出,y的值是x值的2倍,
∴y=2x.

2 [2024 江西中考]将常温中的温度计插入一杯 $ 60^{\circ}C $ 的热水(恒温)中,温度计的读数 $ y(^{\circ}C) $ 与时间 $ x(min) $ 的关系用图象可近似表示为( C )

答案： C 将常温中的温度计插入一杯60℃的热水中,温度计的读数先随着时间增大而升高,达到60℃时,温度计的读数不再发生变化.

3 图书馆现有 1500 本图书供学生借阅,若每个学生一次借 3 本,则剩下的书 $ y $(本)和借书学生人数 $ x $(人)之间的函数关系式是y=1500-3x。

答案： y=1500-3x

如图 1,小亮家、报亭、羽毛球馆在一条直线上.小亮从家跑步到羽毛球馆打羽毛球,再去报亭看报,最后散步回家.小亮离家距离 $ y(km) $ 与时间 $ x(min) $ 之间的函数关系如图 2 所示.下列结论错误的是( D )
A.小亮从家到羽毛球馆用了 7 min
B.小亮从羽毛球馆到报亭平均每分钟走 75 m
C.报亭到小亮家的距离是 400 m
D.小亮打羽毛球的时间是 37 min

答案： D 由题图,得小亮从家到羽毛球馆用了7分钟,小亮从羽毛球馆到报亭的平均速度为(1.0-0.4)÷(45-37)=0.075(km/min)=75(m/min),报亭到小亮家的距离是0.4 km,即400 m,小亮打羽毛球的时间是37-7=30(min),所以选项D中的结论错误,符合题意.

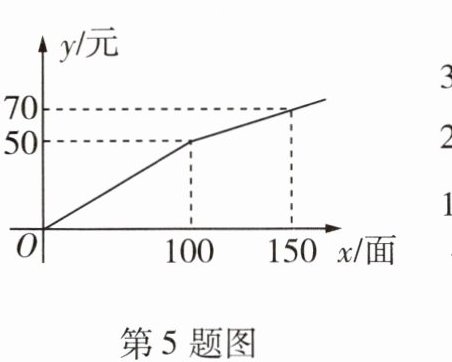
5 某复印店复印收费 $ y $(元)与复印面数 $ x $(面)之间的函数图象如图所示,从图象中可以看出,复印超过 100 面的部分,每面收费0.4元。

答案： 0.4 由题图知,超过100面的部分每面收费(70-50)÷(150-100)=0.4(元).

6 [2024 苏州中学一模]一个装有进水管和出水管的容器,开始时,先打开进水管注水,3 分钟时,打开出水管排水,8 分钟时,关闭进水管,直至容器中的水全部排完.在整个过程中,容器中的水量 $ y $(升)与时间 $ x $(分)之间的函数关系如图所示,则图中 $ a $ 的值为______$\frac{29}{3}$。

答案： $\frac{29}{3}$ 设出水管每分钟排水x升.由题意知,进水管每分钟进水$\frac{30}{3}=10$(升),则有10×8-(8-3)x=20,解得x=12,
∴8分钟后的排水时间为$\frac{20}{12}=\frac{5}{3}$(分),
∴$a=8+\frac{5}{3}=\frac{29}{3}$.

7 [2024 齐齐哈尔中考]在函数 $ y = \frac{1}{\sqrt{3 + x}} + \frac{1}{x + 2} $ 中,自变量 $ x $ 的取值范围是x＞-3且x≠-2。

答案： x＞-3且x≠-2 由题意,得3+x＞0且x+2≠0,解得x＞-3且x≠-2.

(1) $ y $ 与 $ x $ 的函数表达式为y=-2x+35；
(2)求自变量 $ x $ 的取值范围。
由题意，得0＜y≤18.
∵y=-2x+35，
∴$\left\{\begin{array}{l}-2x+35＞0,\\ -2x+35\leqslant 18,\end{array}\right.$解得$\frac{17}{2}\leqslant x＜\frac{35}{2}$，
∴自变量x的取值范围为$\frac{17}{2}\leqslant x＜\frac{35}{2}$.

答案：
(1)y=-2x+35；
(2)由题意，得0＜y≤18.
∵y=-2x+35，
∴$\left\{\begin{array}{l}-2x+35＞0,\\ -2x+35\leqslant 18,\end{array}\right.$解得$\frac{17}{2}\leqslant x＜\frac{35}{2}$，
∴自变量x的取值范围为$\frac{17}{2}\leqslant x＜\frac{35}{2}$.