《2025年一遍过八年级数学上册苏科版》

9 如图,在△ABC中,∠C = 90°,AC = 5cm,CB = 12cm,AB = 13cm,将△ABC沿直线CB向右平移3cm得到△DEF,DF交AB于点G,则点C到直线DE的距离为$\frac{75}{13}$cm.

答案： $\frac{75}{13}$ 如图,过点C作CH⊥DE,交ED的延长线于点H,连接AD,CD.由题意,得DE=AB=13 cm,EF=BC=12 cm,DF=AC=5 cm.
∵CF=3 cm,
∴EC=CF+EF=15 cm.
∵S△CDE=$\frac{1}{2}EC\cdot DF=\frac{1}{2}DE\cdot CH$,
∴CH=$\frac{EC\cdot DF}{DE}=\frac{15×5}{13}=\frac{75}{13}$cm,即点C到直线DE的距离为$\frac{75}{13}$cm.

10 [2025南京将军山中学月考]如图,在△ABC中,∠BAC = 90°,AD是高,BE是中线,CF是角平分线,CF交AD于点G,交BE于点H,给出以下结论:①$S_{△ABE}$ = $S_{△BCE}$;②∠AFG = ∠AGF;③∠FAG = 2∠ACF;④AD·BC = AB·AC.其中正确的有______.(填序号)

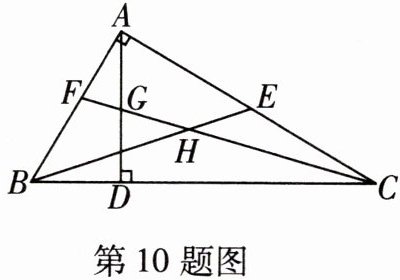
①②③④

答案： ①②③④
∵BE是AC边上的中线,
∴AE=EC,
∴S△ABE=S△BCE,故①正确;
∵CF平分∠ACB,
∴∠ACF=∠BCF=$\frac{1}{2}$∠ACB,
∵∠BAC=90°,
∴∠ACF+∠AFC=90°,
∵AD⊥BC,
∴∠ADC=90°,
∴∠DGC+∠BCF=90°,
∴∠AFC=∠DGC,
∵∠DGC=∠AGF,
∴∠AFG=∠AGF,故②正确;
∵∠BAC=90°,
∴∠BAD+∠DAC=90°,
∵∠ADC=90°,
∴∠DAC+∠ACD=90°,
∴∠BAD=∠ACD,
∵∠ACB=2∠ACF,
∴∠FAG=2∠ACF,故③正确;
∵AD是高,∠BAC=90°,
∴S△ABC=$\frac{1}{2}AD\cdot BC=\frac{1}{2}AB\cdot AC$,
∴AD·BC=AB·AC,故④正确.

11 如图,在△ABC中,D,E,F分别为AB,AC,CD上的一点.
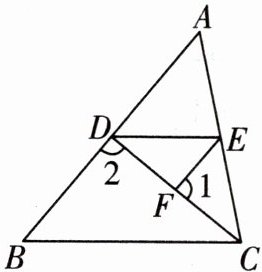
(1)若D,E,F分别为AB,AC,CD的中点,△ABC的面积是16,则四边形ADFE的面积是6;
(2)若∠AED = ∠ACB,∠B = ∠DEF,试说明∠1 + ∠2 = 180°.

如图,延长EF交BC于点G.因为∠AED=∠ACB,所以DE//BC,所以∠DEF=∠EGC.又因为∠B=∠DEF,所以∠B=∠EGC,所以AB//GE,所以∠2+∠DFG=180°.又因为∠1=∠DFG,所以∠1+∠2=180°.

答案：
(1)6 因为F是CD的中点,所以设S△DEF=S△CEF=x.因为E是AC的中点,所以S△ADE=S△CDE=2x.因为D是AB的中点,所以S△ABC=8x=16,所以x=2,所以S四边形ADFE=3x=6.
(2)如图,延长EF交BC于点G.因为∠AED=∠ACB,所以DE//BC,所以∠DEF=∠EGC.又因为∠B=∠DEF,所以∠B=∠EGC,所以AB//GE,所以∠2+∠DFG=180°.又因为∠1=∠DFG,所以∠1+∠2=180°.

12 推理能力 [2024无锡江阴月考]已知在△ABC中,∠BAC = α,BF为△ABC的一条角平分线,过射线AC上一点D(不与点A,C重合)作DE ⊥ BC,垂足为E,射线DG平分∠ADE.
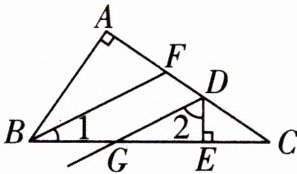
(1)若α = 90°,如图,点D在边AC上,点G在边BC上且不与点B重合.判断∠1与∠2的数量关系,并说明理由.
(2)若0° ＜ α ＜ 90°,射线DG与直线FB交于点H,用含α的代数式表示∠DHF,并说明理由.

答案：
(1)∠1+∠2=90°.理由如下:
∵DE⊥BC,
∴∠DEB=90°.又
∵∠BAC=90°,
∴∠ABE+∠ADE=360°-∠DEB-∠BAC=180°.
∵BF为△ABC的一条角平分线,DG平分∠ADE,
∴$∠1=\frac{1}{2}∠ABE,∠2=\frac{1}{2}∠ADE,$
∴$∠1+∠2=\frac{1}{2}∠ABE+\frac{1}{2}∠ADE=\frac{1}{2}(∠ABE+∠ADE)=\frac{1}{2}×180°=90°.(2)$如图$1,∠DHF=180°-∠HFD-∠ADH=180°-(α+\frac{1}{2}∠ABC)-\frac{1}{2}∠ADE=180°-α-\frac{1}{2}(∠ABC+∠ADE)=180°-α-\frac{1}{2}(360°-90°-α)=180°-α-180°+45°+\frac{1}{2}α=45°-\frac{1}{2}α.$如图$2,∠DHF=180°-(∠HFD+∠FDH)=180°-(180°-α-\frac{1}{2}∠ABC+\frac{1}{2}∠CDE)=α+\frac{1}{2}∠ABC-\frac{1}{2}∠CDE=α+\frac{1}{2}(180°-α-90°+∠CDE)-\frac{1}{2}∠CDE=α+45°-\frac{1}{2}α+\frac{1}{2}∠CDE-\frac{1}{2}∠CDE=45°+\frac{1}{2}α.$综上所述$,∠DHF=45°-\frac{1}{2}α$或$45°+\frac{1}{2}α.$