《2025年一遍过八年级数学上册苏科版》

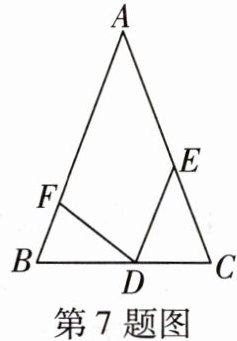
7 [2024南通海安十三校段考]如图,在$\triangle ABC$中,$∠B= ∠C$,$BF= CD$,$BD= CE$. 若$∠A= 40^{\circ }$,则$∠FDE$的度数为(C)

A.$60^{\circ }$
B.$65^{\circ }$
C.$70^{\circ }$
D.$75^{\circ }$

答案： C 在△BFD和△CDE中，{BF=CD，∠B=∠C，BD=CE}，
∴△BFD≌△CDE(SAS)，
∴∠BFD=∠CDE.
∵∠B=∠C，∠A=40°，
∴∠B=∠C=1/2(180° - ∠A)=70°，
∴∠FDB+∠CDE=∠FDB+∠BFD=180° - ∠B=110°，
∴∠FDE=180°-(∠FDB+∠CDE)=180° - 110°=70°.

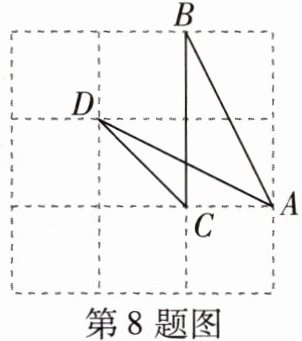
8 [2025常州二十四中期中]如图,在边长为1的正方形网格图中,点$A$,$B$,$C$,$D$均在正方形网格的格点上,则$∠B+∠D= $45$^{\circ }$.

答案： 45 如图，构造△DAE.在△ABC和△DAE中，{AC=DE，∠ACB=∠DEA，BC=AE}，
∴△ABC≌△DAE(SAS)，
∴∠B=∠DAE.
∵∠DCE=∠DAE+∠ADC=45°，
∴∠B+∠ADC=45°.

9 如图,在五边形$ABCDE$中,$AB= AE= 4$,$BC= 3$,$DE= 2$,$∠ABC= ∠AED= 90^{\circ }$,$∠DAC= \frac {1}{2}∠BAE$,则五边形$ABCDE$的面积为____20.

答案： 20 解题思路：将△ABC绕点A顺时针旋转至△AEF，由∠B=∠AEF=∠AED=90°，得∠DEF=180°，即D，E，F三点共线，易证△ACD≌△AFD，可得结论.如图，将△ABC绕点A顺时针旋转至△AEF（旋转构造全等三角形），则AF=AC，∠B=∠AEF=∠AED=90°，
∴∠DEF=180°，即D，E，F三点共线.
∵∠DAC=1/2∠BAE=∠DAE+∠BAC，∠DAE+∠BAC=∠DAE+∠EAF=∠FAD，
∴∠CAD=∠FAD.在△ACD和△AFD中，{AC=AF，∠CAD=∠FAD，AD=AD}，
∴△ACD≌△AFD（SAS），
∴S△ACD=S△AFD=S△AED+S△ABC=1/2×4×2+1/2×4×3=10，
∴S五边形ABCDE=2S△ACD=20.

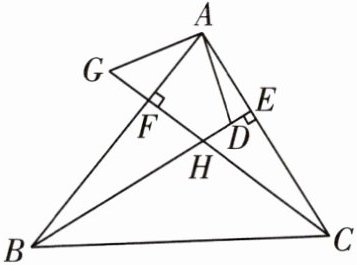
10 如图,在$\triangle ABC$中,$BE$,$CF分别是AC$,$AB$边上的高,在$BE上截取BD= AC$,在$CF的延长线上截取CG= AB$,连接$AD$,$AG$.
(1)求证：$AD= AG$.
(2)$AD与AG$的位置关系如何？请说明理由.

答案：
(1)证明：
∵BE⊥AC，CF⊥AB，
∴∠HEC=∠HFB=90°.又
∵∠CHE=∠BHF，
∴∠ACG=∠ABD.在△ABD和△GCA中，{AB=GC，∠ABD=∠GCA，BD=CA}，
∴△ABD≌△GCA(SAS)，
∴AD=AG.
(2)解：AD⊥AG.理由如下.
∵△ABD≌△GCA，
∴∠ADB=∠GAC.又
∵∠ADB=∠AED+∠DAE，∠GAC=∠GAD+∠DAE，
∴∠GAD=∠AED=90°，
∴AD⊥AG.

11 推理能力 某数学兴趣小组在一次活动中进行了探究活动,请你来加入.
【探究与发现】
(1)如图1,$AD是\triangle ABC$的中线,延长$AD至点E$,使$ED= AD$,连接$BE$. 求证：$\triangle ACD\cong \triangle EBD$.
证明：
∵AD是△ABC的中线，
∴CD=BD.在△ACD和△EBD中，{CD=BD，∠ADC=∠EDB，AD=ED}，
∴△ACD≌△EBD(SAS).
【理解与应用】
(2)如图2,$EP是\triangle DEF$的中线. 若$EF= 5$,$DE= 3$,则$EP$的取值范围是____.
1＜EP＜4
(3)如图3,$AD是\triangle ABC$的中线,点$E$,$F分别在AB$,$AC$上,且$DE⊥DF于点D$. 求证：$BE+CF＞EF$.
证明：如图2，延长FD至点G，使GD=DF，连接BG，EG.
∵AD是△ABC的中线，
∴DC=DB.在△DFC和△DGB中，{DF=DG，∠CDF=∠BDG，DC=DB}，
∴△DFC≌△DGB(SAS)，
∴CF=BG.
∵DE⊥DF，
∴∠FDE=∠GDE=90°.在△EDF和△EDG中，{DF=DG，∠FDE=∠GDE=90°，DE=DE}，
∴△EDF≌△EDG(SAS)，
∴EF=EG.在△BEG中，BE+BG＞EG.
∵EF=EG，CF=BG，
∴BE+CF＞EF.

答案：
(1)证明：
∵AD是△ABC的中线，
∴CD=BD.在△ACD和△EBD中，{CD=BD，∠ADC=∠EDB，AD=ED}，
∴△ACD≌△EBD(SAS).
(2)解：1＜EP＜4 如图1，延长EP至点Q，使PQ=PE，连接FQ.
∵EP是△DEF的中线，
∴PD=PF.在△PDE和△PFQ中，{PE=PQ，∠EPD=∠QPF，PD=PF}，
∴△PDE≌△PFQ(SAS)，
∴FQ=DE=3.在△EFQ中，EF - FQ＜QE＜EF+FQ，即5 - 3＜2EP＜5+3，
∴1＜EP＜4.
(3)证明：如图2，延长FD至点G，使GD=DF，连接BG，EG.
∵AD是△ABC的中线，
∴DC=DB.在△DFC和△DGB中，{DF=DG，∠CDF=∠BDG，DC=DB}，
∴△DFC≌△DGB(SAS)，
∴CF=BG.
∵DE⊥DF，
∴∠FDE=∠GDE=90°.在△EDF和△EDG中，{DF=DG，∠FDE=∠GDE=90°，DE=DE}，
∴△EDF≌△EDG(SAS)，
∴EF=EG.在△BEG中，BE+BG＞EG.
∵EF=EG，CF=BG，
∴BE+CF＞EF.