《2025年一遍过八年级数学上册苏科版》

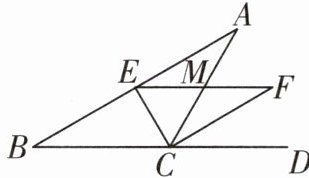
9 [2025徐州铜山区期中]如图,CE是△ABC的角平分线,过点E作EF//BC,分别交AC及△ABC的外角∠ACD的平分线于点M,F.若CM= 3,则$CE^2+CF^2$的值为 (A)

A.36
B.9
C.6
D.18

答案： A
∵CE是∠ACB的平分线,CF是∠ACD的平分线,
∴∠ACE = ∠BCE = 1/2∠ACB,∠ACF = ∠DCF = 1/2∠ACD.
∵∠ACB + ∠ACD = 180°,
∴∠ACE + ∠ACF = 1/2(∠ACB + ∠ACD)=1/2×180° = 90°,即∠ECF = 90°,
∴CE² + CF² = EF².
∵EF//BC,
∴∠MEC = ∠BCE,∠MFC = ∠DCF,
∴∠MEC = ∠ACE,∠MFC = ∠ACF,
∴EM = CM = 3,FM = CM = 3,
∴EF = EM + FM = 3 + 3 = 6,
∴CE² + CF² = 6² = 36.

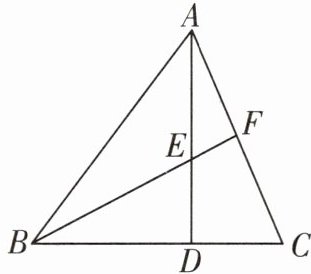
10 如图,在△ABC中,AD⊥BC于点D,BF平分∠ABC交AD于点E,交AC于点F,AC= 13,AD= 12,BC= 14,则DE的长等于 (A)

A.9/2
B.5
C.13/2
D.7

答案： A
∵AD⊥BC,
∴∠ADC = ∠ADB = 90°,
∴CD = √(AC² - AD²)=√(13² - 12²)=5,
∴BD = BC - CD = 14 - 5 = 9.
∵∠ADB = 90°,
∴AB = √(AD² + BD²)=√(12² + 9²)=15.如图,过点E作EG⊥AB于点G.
∵BF平分∠ABC,AD⊥BC,EG⊥AB,
∴EG = ED.在Rt△BDE和Rt△BGE中,{BE = BE,ED = EG,
∴Rt△BDE≌Rt△BGE(HL),
∴BG = BD = 9,
∴AG = AB - BG = 15 - 9 = 6.设AE = x,则ED = 12 - x,
∴EG = 12 - x.在Rt△AGE中,由勾股定理,得AG² + EG² = AE²,
∴6² + (12 - x)² = x²,解得x = 15/2,
∴AE = 15/2,
∴DE = AD - AE = 12 - 15/2 = 9/2.

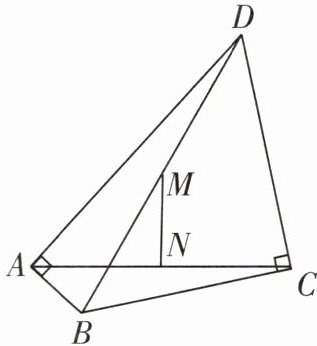
11 [2025南京联合体期末]如图,在四边形ABCD中,∠BAD= ∠BCD= 90°,M,N分别是对角线BD,AC的中点.若AC= 6,BD= 8,则MN的长为______.

√7

答案： √7 如图,连接AM,CM.
∵∠BAD = ∠BCD = 90°,M是BD的中点,
∴AM = CM = 1/2BD = 4.又
∵N是AC的中点,
∴MN⊥AC,AN = CN = 1/2AC = 3.在Rt△ANM中,由勾股定理,得MN² = AM² - AN² = 4² - 3² = 7,
∴MN = √7.

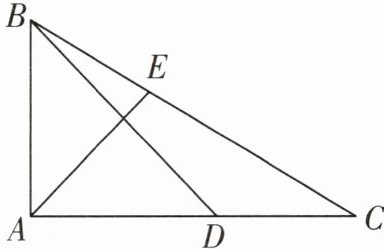
12 [2025盐城中学月考]如图,在Rt△ABC中,∠BAC= 90°,AB= 3,AC= 5,点D是AC边上的动点,点E是BC边上的动点,且保持CD= BE,则$(AE+BD)^2$的最小值为______43.

答案： 43 如图,过点B作BF//AC,使BF = BC,连接EF,AF.
∵BF//AC,
∴∠C = ∠EBF.又
∵BC = BF,CD = BE,
∴△CDB≌△BEF(SAS),
∴BD = EF,
∴AE + BD = AE + EF,
∴当A,E,F三点共线时,AE + BD的值最小.
∵BC = √(AB² + AC²)=√(3² + 5²)=√34,
∴BF = BC = √34.
∵BF//AC,∠BAC = 90°,
∴∠ABF = 90°,
∴AF = √(AB² + BF²)=√(3² + (√34)²)=√43,
∴(AE + BD)²的最小值为(√43)² = 43.

13 推理能力[2025南京联合体期中]在△ABC中,BC= a,AC= b,AB= c.如图1,当∠C= 90°时$,a^2+b^2= c^2.$
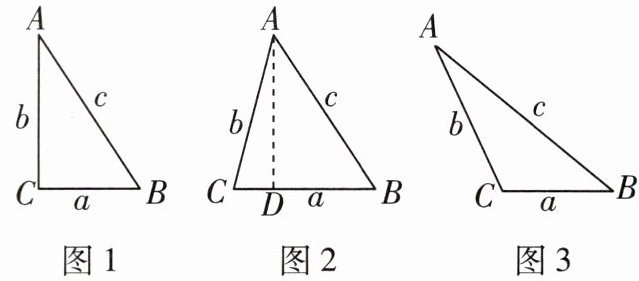
(1)如图2,当∠C＜90°时,小明猜想$a^2+b^2＞c^2.$理由如下:过点A作AD⊥BC,垂足为D,则∠ADC= ∠ADB= 90°.设CD= x……完成小明的证明过程;
(2)如图3,当∠C＞90°时,猜想$a^2+b^2$与$c^2$的大小关系,并证明你的猜想.
]

答案： 解:
(1)过点A作AD⊥BC,垂足为D,则∠ADC = ∠ADB = 90°.设CD = x,由勾股定理,得AD² = b² - x²,AD² = c² - (a - x)²,
∴b² - x² = c² - (a - x)²,
∴a² + b² = c² + 2ax.
∵a ＞ 0,x ＞ 0,
∴2ax ＞ 0,
∴a² + b² ＞ c².
(2)当∠C ＞ 90°时,a² + b²与c²的大小关系为a² + b² ＜ c².证明:如图,过点A作AD⊥BC,交BC的延长线于点D,则∠D = 90°.设CD = x.由勾股定理,得AD² = AC² - DC² = b² - x²,AD² = AB² - BD² = c² - (a + x)²,
∴b² - x² = c² - (a + x)²,
∴a² + b² = c² - 2ax.
∵a ＞ 0,x ＞ 0,
∴2ax ＞ 0,
∴a² + b² ＜ c².