《2025年一遍过八年级数学上册苏科版》

13 对于不相等的两个数a,b,定义$min\{ a,b\}$的含义为:当$a\lt b$时,$min\{ a,b\} = a$;当$a＞b$时,$min\{ a,b\} = b$.例如:$min\{ 1,-2\} = -2$.已知$min\{ \sqrt {29},a\} = a,min\{ \sqrt {34},b\} = \sqrt {34}$,且a和b为两个连续正整数,则$3a-2b$的值为3.

答案： 3 由题意,得$a＜\sqrt{29}$,$b＞\sqrt{34}$.$\because 5＜\sqrt{29}＜6$,$5＜\sqrt{34}＜6$,$a$和$b$为两个连续正整数,$\therefore a=5$,$b=6$,$\therefore 3a-2b=3× 5-2× 6=15-12=3$.

14 一个数值转换器的原理如图所示.
[img]

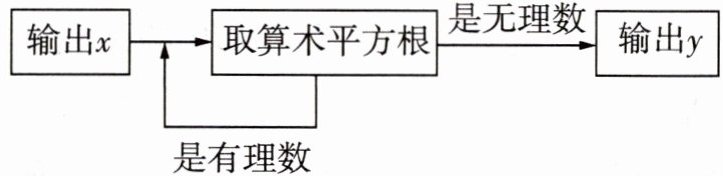
(1)当输入的x值为16时,求输出的y值.
解:当$x=16$时,$\sqrt{16}=4$(有理数),$\sqrt{4}=2$(有理数),$\sqrt{2}$是无理数,$\therefore y=\sqrt{2}$.
(2)是否存在输入的x值后,始终输不出y值?如果存在,请直接写出所有满足要求的x值;如果不存在,请说明理由.
解:存在.$x=0$或1或负数.
(3)输入一个两位数x,恰好经过两次取算术平方根才能输出无理数,则这个两位数x是____.25或36或49或64

答案： 解:
(1)当$x=16$时,$\sqrt{16}=4$(有理数),$\sqrt{4}=2$(有理数),$\sqrt{2}$是无理数,$\therefore y=\sqrt{2}$.
(2)存在.$x=0$或1或负数.
(3)25或36或49或64$x=[(\sqrt{5})^{2}]^{2}=25$或$x=[(\sqrt{6})^{2}]^{2}=36$或$x=[(\sqrt{7})^{2}]^{2}=49$或$x=[(\sqrt{8})^{2}]^{2}=64$.

15 推理能力 定义:若无理数$\sqrt {T}$的被开方数(T为正整数)满足$n^{2}\lt T＜(n+1)^{2}$(其中n为正整数),则称无理数$\sqrt {T}$的“共同体区间”为$(n,n+1)$.例如:因为$1^{2}＜3＜2^{2}$,所以$\sqrt {3}$的“共同体区间”为$(1,2)$.请回答下列问题:
(1)$\sqrt {26}$的“共同体区间”为(5,6);
(2)若无理数$\sqrt {a}$的“共同体区间”为$(2,3)$,求$\sqrt {a+6}$的“共同体区间”;
解:$\because$无理数$\sqrt{a}$的“共同体区间”为$(2,3)$,$\therefore 2^{2}＜a＜3^{2}$,即$4＜a＜9$,$\therefore 10＜a+6＜15$,$\therefore 3^{2}＜a+6＜4^{2}$,$\therefore \sqrt{a+6}$的“共同体区间”为$(3,4)$.
(3)若整数x,y满足关系式:$\sqrt {x-3}+|2023+(y-4)^{2}|= 2024$,求$\sqrt {x(y+1)}$的“共同体区间”.
解:$\because \sqrt{x-3}+\vert 2023+(y-4)^{2}\vert =2024$,$\therefore \left\{\begin{array}{l} \sqrt{x-3}=1,\\ (y-4)^{2}=0\end{array}\right. $或$\left\{\begin{array}{l} \sqrt{x-3}=0,\\ (y-4)^{2}=1,\end{array}\right. $解得$\left\{\begin{array}{l} x=4,\\ y=4\end{array}\right. $或$\left\{\begin{array}{l} x=3,\\ y=5\end{array}\right. $或$\left\{\begin{array}{l} x=3,\\ y=3.\end{array}\right. $当$x=4,y=4$时,$x(y+1)=20$,$\because 4^{2}＜20＜5^{2}$,$\therefore \sqrt{x(y+1)}$的“共同体区间”为$(4,5)$.当$x=3,y=5$时,$x(y+1)=18$,$\because 4^{2}＜18＜5^{2}$,$\therefore \sqrt{x(y+1)}$的“共同体区间”为$(4,5)$.当$x=3,y=3$时,$x(y+1)=12$,$\because 3^{2}＜12＜4^{2}$,$\therefore \sqrt{x(y+1)}$的“共同体区间”为$(3,4)$.综上可知,$\sqrt{x(y+1)}$的“共同体区间”为$(4,5)$或$(3,4)$.

答案： 解:
(1)$(5,6)$$\because 5^{2}＜26＜6^{2}$,$\therefore \sqrt{26}$的“共同体区间”是$(5,6)$.
(2)$\because$无理数$\sqrt{a}$的“共同体区间”为$(2,3)$,$\therefore 2^{2}＜a＜3^{2}$,即$4＜a＜9$,$\therefore 10＜a+6＜15$,$\therefore 3^{2}＜a+6＜4^{2}$,$\therefore \sqrt{a+6}$的“共同体区间”为$(3,4)$.
(3)$\because \sqrt{x-3}+\vert 2023+(y-4)^{2}\vert =2024$,$\therefore \left\{\begin{array}{l} \sqrt{x-3}=1,\\ (y-4)^{2}=0\end{array}\right. $或$\left\{\begin{array}{l} \sqrt{x-3}=0,\\ (y-4)^{2}=1,\end{array}\right. $解得$\left\{\begin{array}{l} x=4,\\ y=4\end{array}\right. $或$\left\{\begin{array}{l} x=3,\\ y=5\end{array}\right. $或$\left\{\begin{array}{l} x=3,\\ y=3.\end{array}\right. $当$x=4,y=4$时,$x(y+1)=20$,$\because 4^{2}＜20＜5^{2}$,$\therefore \sqrt{x(y+1)}$的“共同体区间”为$(4,5)$.当$x=3,y=5$时,$x(y+1)=18$,$\because 4^{2}＜18＜5^{2}$,$\therefore \sqrt{x(y+1)}$的“共同体区间”为$(4,5)$.当$x=3,y=3$时,$x(y+1)=12$,$\because 3^{2}＜12＜4^{2}$,$\therefore \sqrt{x(y+1)}$的“共同体区间”为$(3,4)$.综上可知,$\sqrt{x(y+1)}$的“共同体区间”为$(4,5)$或$(3,4)$.

【思考】有理数和无理数有什么区别?

答案： 【解析】：
本题主要考察有理数和无理数的定义及其区别。
有理数是可以表示为两个整数的比的数，即形如$\frac{p}{q}$（$q \neq 0$）的数，包括整数、有限小数和无限循环小数。
无理数则不能表示为两个整数的比，它们是无限不循环的小数，如$\pi$、$e$等。
【答案】：
有理数是可以表示为两个整数的比的数，包括整数、有限小数和无限循环小数；
无理数则不能表示为两个整数的比，是无限不循环的小数。