第71页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
台风是以台风中心为圆心,可以在周围上千 米的范围内形成的极端气候,有极强的破坏力. 某 市夏季受到台风天气的影响,如图1,点A为该市的某观测站,点C为该市的某海港,此时观测 到有一台风中心B在观测站A的正东方向正继续向西移动.

(1)若$AC= 300km,BC= 400km,AB= 500km,$ 判断$△ABC$的形状.
(2)在(1)的条件下,若以台风中心为圆心,周围 250 km 以内为受影响区域,则海港C受台风 影响吗?并说明理由.
(3)在(2)的条件下,若台风的速度为35 km/h, 则台风影响海港C持续的时间有多长?
(4)在海港C的水平地面上有许多图案,图2是 其中之一,它可以看成是由四个全等的直角 三角形无缝隙无重叠地拼接在一起的.如图 3,若图形ABCDEFGH的周长为80 m,$OB= 5m$,求该图形的面积S.

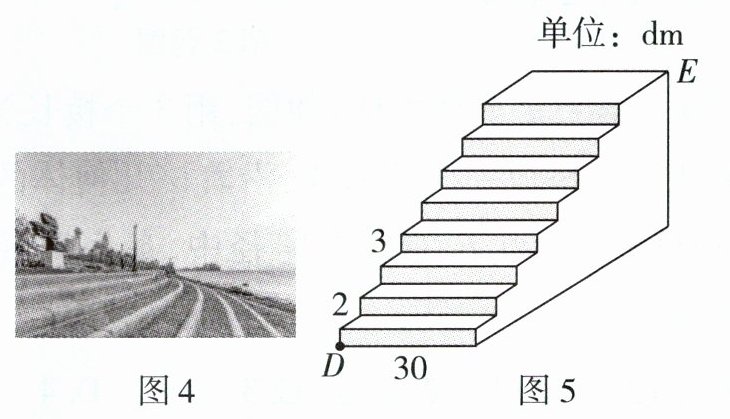
(5)图4是海港C附近的江滩台阶,共有8级, 每一级的长、宽、高分别为30 dm,3 dm, 2 dm,图5是其示意图.已知D和E是该台 阶上两个相对的点,若点D处有一只乌龟, 当台风来临时,为快速爬到点E处的绿植中 躲避台风,求该乌龟沿台阶面爬到点E的最 短路程.

(1)若$AC= 300km,BC= 400km,AB= 500km,$ 判断$△ABC$的形状.
(2)在(1)的条件下,若以台风中心为圆心,周围 250 km 以内为受影响区域,则海港C受台风 影响吗?并说明理由.
(3)在(2)的条件下,若台风的速度为35 km/h, 则台风影响海港C持续的时间有多长?
(4)在海港C的水平地面上有许多图案,图2是 其中之一,它可以看成是由四个全等的直角 三角形无缝隙无重叠地拼接在一起的.如图 3,若图形ABCDEFGH的周长为80 m,$OB= 5m$,求该图形的面积S.

(5)图4是海港C附近的江滩台阶,共有8级, 每一级的长、宽、高分别为30 dm,3 dm, 2 dm,图5是其示意图.已知D和E是该台 阶上两个相对的点,若点D处有一只乌龟, 当台风来临时,为快速爬到点E处的绿植中 躲避台风,求该乌龟沿台阶面爬到点E的最 短路程.

答案:
(1)解:
∵AC²+BC²=300²+400²=250000,AB²=500²=250000,
∴AC²+BC²=AB²,
∴△ABC是直角三角形。
(2)解:海港C受台风影响。理由:过点C作CD⊥AB于点D,S△ABC=1/2×AC×BC=1/2×AB×CD,即1/2×300×400=1/2×500×CD,解得CD=240km。
∵240<250,
∴海港C受台风影响。
(3)解:设台风中心移动到点E、F时,CE=CF=250km,在Rt△CDE中,DE=√(CE²-CD²)=√(250²-240²)=70km,同理DF=70km,EF=DE+DF=140km,时间t=140÷35=4h,即台风影响海港C持续的时间为4h。
(4)解:设直角三角形的短直角边为a,长直角边为b,由OB=5m得b-a=5。图形周长为8(b+a)=80,即b+a=10。联立得a=2.5,b=7.5。S=4×1/2×a×b + (b-a)²=4×1/2×2.5×7.5 + 5²=37.5 + 25=62.5m²。
(5)解:将台阶展开,水平总宽=8×3=24dm,垂直总高=8×2=16dm,水平长30dm,展开后直角三角形两直角边分别为30dm和24+16=40dm,最短路程=√(30²+40²)=50dm。
(1)解:
∵AC²+BC²=300²+400²=250000,AB²=500²=250000,
∴AC²+BC²=AB²,
∴△ABC是直角三角形。
(2)解:海港C受台风影响。理由:过点C作CD⊥AB于点D,S△ABC=1/2×AC×BC=1/2×AB×CD,即1/2×300×400=1/2×500×CD,解得CD=240km。
∵240<250,
∴海港C受台风影响。
(3)解:设台风中心移动到点E、F时,CE=CF=250km,在Rt△CDE中,DE=√(CE²-CD²)=√(250²-240²)=70km,同理DF=70km,EF=DE+DF=140km,时间t=140÷35=4h,即台风影响海港C持续的时间为4h。
(4)解:设直角三角形的短直角边为a,长直角边为b,由OB=5m得b-a=5。图形周长为8(b+a)=80,即b+a=10。联立得a=2.5,b=7.5。S=4×1/2×a×b + (b-a)²=4×1/2×2.5×7.5 + 5²=37.5 + 25=62.5m²。
(5)解:将台阶展开,水平总宽=8×3=24dm,垂直总高=8×2=16dm,水平长30dm,展开后直角三角形两直角边分别为30dm和24+16=40dm,最短路程=√(30²+40²)=50dm。
查看更多完整答案,请扫码查看


