《2025年轻松作业本九年级数学上册苏科版》

5. 甲、乙、丙、丁四位运动员参加男子100m自由泳选拔赛,他们5次比赛的平均成绩$\overline {x}和方差s^{2}$如下表所示：

若要选拔一名速度快且发挥稳定的运动员参加比赛,根据表中数据应选择 (A)
A. 甲
B. 乙
C. 丙
D. 丁

答案： A

6. 某工程队有14名员工,他们的工种及相应每人每月工资如下表所示：

现该工程队进行了人员调整：减少木工2名,增加电工、瓦工各1名,与调整前相比,该工程队员工月工资的方差____变大. (填“变小”“不变”或“变大”)

答案： 变大

7. 某体校准备从甲、乙、丙三位同学中选拔一人参加全市射击比赛. 他们在选拔比赛中,射靶10次的平均环数是$\overline {x}_{甲}= \overline {x}_{乙}= \overline {x}_{丙}= 8.3$,方差分别是$s^{2}_{甲}= 1.5$,$s^{2}_{乙}= 2.8$,$s^{2}_{丙}= 3.2$,那么根据以上提供的信息,你认为应该推荐参加全市射击比赛的同学是甲.

答案： 甲

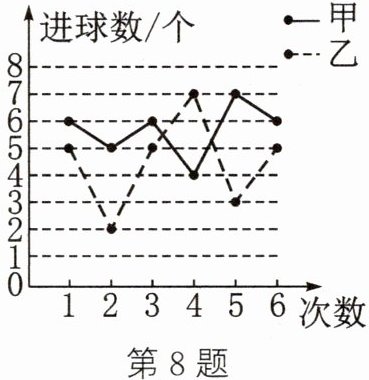
8. 如图是甲、乙两位选手6次投篮测试(每次投篮10个)成绩的统计图,我们可以判断甲选手的成绩更稳定. (填“甲”或“乙”)

答案： 甲

9. 周老师平时上班有A、B两条路线可以选择,她记录了两周共10天的上班路上所用的时间并绘制了统计图如图所示：
(1) 这10天中周老师上班路上所用时间最多相差22min；
(2) 哪一条上班路线用时更稳定？请通过计算说明；
(3) 你建议周老师应如何选择上班路线？
(2) 路线 A 所用时间的平均数为 $ \frac{40 + 22 + 21 + 19 + 18}{5} = 24 $ (min)，方差为 $ \frac{1}{5} × [(40 - 24)^2 + (22 - 24)^2 + (21 - 24)^2 + (19 - 24)^2 + (18 - 24)^2] = 66 $，路线 B 所用时间的平均数为 $ \frac{30 + 27 + 26 + 25 + 27}{5} = 27 $ (min)，方差为 $ \frac{1}{5} × [(30 - 27)^2 + (27 - 27)^2 + (26 - 27)^2 + (25 - 27)^2 + (27 - 27)^2] = 2.8 $，∵ $ 66 ＞ 2.8 $，∴ 上班路线 B 用时更稳定；
(3) 由用时的平均数知，路线 A 平均用时更少，所以建议选择路线 A (答案不唯一，合理即可).

答案：
(1) 22
(2) 路线 A 所用时间的平均数为 $ \frac{40 + 22 + 21 + 19 + 18}{5} = 24 $ (min)，方差为 $ \frac{1}{5} × [(40 - 24)^2 + (22 - 24)^2 + (21 - 24)^2 + (19 - 24)^2 + (18 - 24)^2] = 66 $，路线 B 所用时间的平均数为 $ \frac{30 + 27 + 26 + 25 + 27}{5} = 27 $ (min)，方差为 $ \frac{1}{5} × [(30 - 27)^2 + (27 - 27)^2 + (26 - 27)^2 + (25 - 27)^2 + (27 - 27)^2] = 2.8 $，
∵ $ 66 ＞ 2.8 $，
∴ 上班路线 B 用时更稳定；
(3) 由用时的平均数知，路线 A 平均用时更少，所以建议选择路线 A (答案不唯一，合理即可).