第78页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
6. 学校食堂有10元、12元、15元三种价位的午餐供学生选择(每人购一份),某天午餐销售情况如图所示,则当天学生购买午餐的平均费用是 (

A. 10.8元
B. 11.8元
C. 12.6元
D. 13.6元
B
)
A. 10.8元
B. 11.8元
C. 12.6元
D. 13.6元
答案:
B
7. 学校要选拔学生会主席,对人围的A、B两名候选人进行了两项素质测试,两人的两项测试成绩如表所示.根据实际需要,将面试、综合知识测试的得分按3:2的比例计算两人的总成绩,那么______
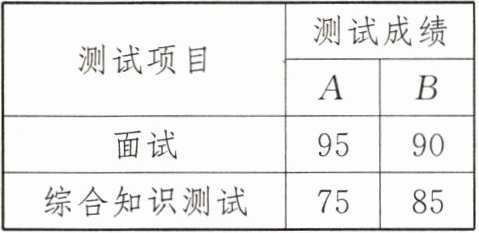
B
(填“A”或“B”)将被录用.
答案:
B
8. 某校招聘一名数学老师,对应聘者分别进行了教学能力、科研能力和组织能力三项测试,其中甲、乙两名应聘者的成绩如右表所示:(单位:分)
| | 教学能力 | 科研能力 | 组织能力 |
|--|--|--|--|
| 甲 | 81 | 85 | 86 |
| 乙 | 92 | 80 | 74 |
(1)若根据三项测试的平均成绩在甲、乙两人中录用一人,那么谁将被录用?
(2)根据实际需要,学校将教学、科研和组织能力三项测试得分按5:3:2的比确定每人的最后成绩,若按此成绩在甲、乙两人中录用一人,谁将被录用?
| | 教学能力 | 科研能力 | 组织能力 |
|--|--|--|--|
| 甲 | 81 | 85 | 86 |
| 乙 | 92 | 80 | 74 |
(1)若根据三项测试的平均成绩在甲、乙两人中录用一人,那么谁将被录用?
(2)根据实际需要,学校将教学、科研和组织能力三项测试得分按5:3:2的比确定每人的最后成绩,若按此成绩在甲、乙两人中录用一人,谁将被录用?
答案:
解:
(1) 甲的平均成绩为 $ \frac{81 + 85 + 86}{3} = 84 $ (分);乙的平均成绩为 $ \frac{92 + 80 + 74}{3} = 82 $ (分),因为甲的平均成绩高于乙的平均成绩,所以甲被录用;
(2) 根据题意,甲的平均成绩为 $ \frac{81 × 5 + 85 × 3 + 86 × 2}{5 + 3 + 2} = 83.2 $ (分),乙的平均成绩为 $ \frac{92 × 5 + 80 × 3 + 74 × 2}{5 + 3 + 2} = 84.8 $ (分),因为甲的平均成绩低于乙的平均成绩,所以乙被录用.
(1) 甲的平均成绩为 $ \frac{81 + 85 + 86}{3} = 84 $ (分);乙的平均成绩为 $ \frac{92 + 80 + 74}{3} = 82 $ (分),因为甲的平均成绩高于乙的平均成绩,所以甲被录用;
(2) 根据题意,甲的平均成绩为 $ \frac{81 × 5 + 85 × 3 + 86 × 2}{5 + 3 + 2} = 83.2 $ (分),乙的平均成绩为 $ \frac{92 × 5 + 80 × 3 + 74 × 2}{5 + 3 + 2} = 84.8 $ (分),因为甲的平均成绩低于乙的平均成绩,所以乙被录用.
9. 某公司招聘职员两名,对甲、乙、丙、丁四名候选人进行了笔试和面试,各项成绩满分均为100分,然后按笔试占60%,面试占40%计算候选人的综合成绩(满分为100分),他们的各项成绩如右表所示:
| 候选人 | 笔试成绩/分 | 面试成绩/分 |
|--|--|--|
| 甲 | 90 | 88 |
| 乙 | 84 | 92 |
| 丙 | $ x $ | 90 |
| 丁 | 88 | 86 |
(1)这四名候选人面试成绩的平均数是
(2)现得知候选人丙的综合成绩为87.6分,则表中$ x $的值为
(3)求其余三名候选人的综合成绩,并以综合成绩排序确定所要招聘的前两名的人选.
甲候选人的综合成绩为89.2分,乙候选人的综合成绩为87.2分,丁候选人的综合成绩为87.2分,以综合成绩排序确定所要招聘的前两名的人选是甲和丙.
| 候选人 | 笔试成绩/分 | 面试成绩/分 |
|--|--|--|
| 甲 | 90 | 88 |
| 乙 | 84 | 92 |
| 丙 | $ x $ | 90 |
| 丁 | 88 | 86 |
(1)这四名候选人面试成绩的平均数是
89分
;(2)现得知候选人丙的综合成绩为87.6分,则表中$ x $的值为
86
;(3)求其余三名候选人的综合成绩,并以综合成绩排序确定所要招聘的前两名的人选.
甲候选人的综合成绩为89.2分,乙候选人的综合成绩为87.2分,丁候选人的综合成绩为87.2分,以综合成绩排序确定所要招聘的前两名的人选是甲和丙.
答案:
解:
(1) 89 分
(2) 86
(3)
∵ 甲候选人的综合成绩为 $ 90 × 60\% + 88 × 40\% = 89.2 $ (分),乙候选人的综合成绩为 $ 84 × 60\% + 92 × 40\% = 87.2 $ (分),丁候选人的综合成绩为 $ 88 × 60\% + 86 × 40\% = 87.2 $ (分),
∴ 以综合成绩排序确定所要招聘的前两名的人选是甲和丙.
(1) 89 分
(2) 86
(3)
∵ 甲候选人的综合成绩为 $ 90 × 60\% + 88 × 40\% = 89.2 $ (分),乙候选人的综合成绩为 $ 84 × 60\% + 92 × 40\% = 87.2 $ (分),丁候选人的综合成绩为 $ 88 × 60\% + 86 × 40\% = 87.2 $ (分),
∴ 以综合成绩排序确定所要招聘的前两名的人选是甲和丙.
查看更多完整答案,请扫码查看


