《2025年轻松作业本九年级数学上册苏科版》

8. 如图,在矩形ABCD内有一动点P,且∠BPC = 135°,AB = 3,BC = 4,则AP长的最小值为$ \sqrt { 29 } - 2 \sqrt { 2 } $.

答案： $ \sqrt { 29 } - 2 \sqrt { 2 } $

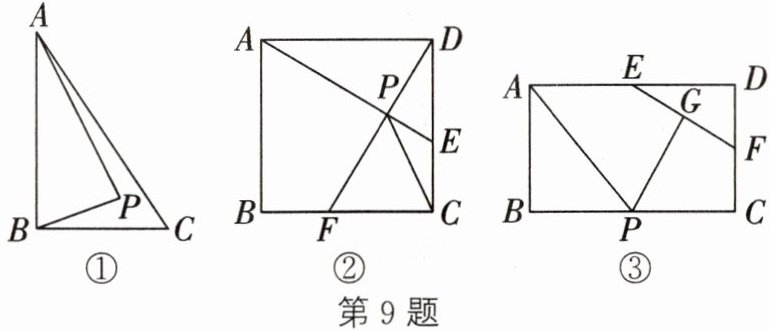
9. 我们在学习圆的知识时,常常碰到题目中明明没有圆,但解决问题时要用到,这就是所谓的"隐圆"问题:
下面让我们一起尝试去解决:
(1) 如图①,在Rt△ABC中,AB⊥BC,AB = 6,BC = 4,P是△ABC内部的一个动点,且满足∠PAB = ∠PBC,则线段CP长的最小值为______;
(2) 如图②,在正方形ABCD中,动点E、F分别从D、C两点同时出发,以相同的速度在边DC、CB上移动,连接AE和DF交于点P,由于点E、F的移动,使得点P也随之运动.若AD = 2,则线段CP的最小值是______;
(3) 如图③,在矩形ABCD中,AB = 2,AD = 3,点E、F分别为AD、DC边上的点,且EF = 2,点G为EF的中点,点P为BC上一动点,则PA + PG的最小值为多少?

答案：

(1) 2　
(2) $ \sqrt { 5 } - 1 $
(3) 如图, 连接 $DG$. $ \because EF = 2 $, 点 $G$ 为 $EF$ 的中点, $ \therefore DG = 1 $. $ \therefore $ 点 $G$ 是以 $D$ 为圆心, 1 为半径的圆弧上的点, 作点 $A$ 关于 $BC$ 的对称点 $A ^ { \prime }$, 连接 $A ^ { \prime }D$, 交 $BC$ 于点 $P$, 交以点 $D$ 为圆心, 1 为半径的圆于点 $G$, 此时 $PA + PG$ 的值最小, 最小值为 $A ^ { \prime }G$ 的长. $ \because AB = 2, AD = 3 $, $ \therefore AA ^ { \prime } = 4 $. $ \therefore A ^ { \prime }D = 5 $. $ \therefore A ^ { \prime }G = A ^ { \prime }D - DG = 5 - 1 = 4 $. $ \therefore PA + PG$ 的最小值为 4.