《2025年轻松作业本九年级数学上册苏科版》

9. 将边长为2的小正方形$ABCD$和边长为4的大正方形$EFGH$按如图所示摆放,使得$C$、$E$两点刚好重合,且$B$、$C$、$H$三点共线,此时经过$A$、$F$、$G$三点作一个圆,则该圆的半径为$2\sqrt{5}$.

答案： $2\sqrt{5}$

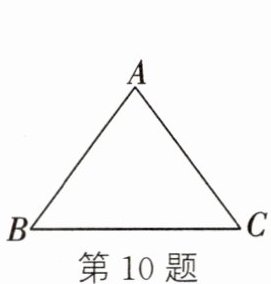
10. 如图,在$\triangle ABC$中,$AB = AC = 5$,$BC = 6$.$\odot O经过B$、$C$两点,且$AO = 3$,则$\odot O$的半径长是$\sqrt{10}$或$\sqrt{58}$.

答案： $\sqrt{10}$或　$\sqrt{58}$

11. 已知坐标平面内有$A$、$B$、$C$三点,且点$A$、$B$、$C的坐标分别为A(3,7)$、$B(-1,-5)$、$C(1,1)$.试确定过$A$、$B$、$C$三点是否能确定一个圆,并说明你的理由.

答案： 解:不能.理由:设直线AB的表达式为y = kx + b，由点A(3,7)、B(-1,-5)，可以求得y = 3x - 2.当x = 1时，y = 1，即点C在直线AB上.因此点A、B、C在同一直线上，
∴过A、B、C三点不能够确定一个圆.

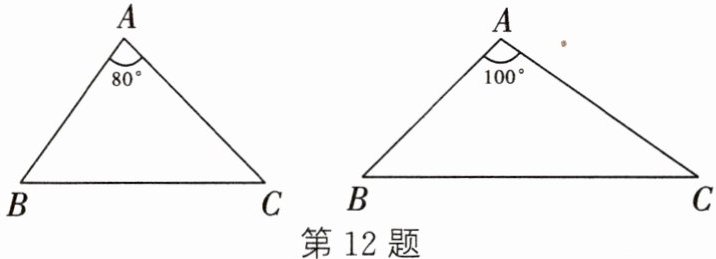
12. 我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆.例如线段$AB的最小覆盖圆就是以线段AB$为直径的圆.
(1) 请分别作出下图中两个三角形的最小覆盖圆(要求用尺规作图,保留作图痕迹,不写作法);
(2) 探究三角形的最小覆盖圆有何规律,请写出你所得到的结论(不要求证明).

答案：

(1)如图所示　
(2)锐角三角形和直角三角形的最小覆盖圆是其外接圆;钝角三角形的最小覆盖圆是以其最长边为直径的圆

13. 在$\triangle ABC和\triangle ADE$中,$AB = AC$,$AD = AE$,$\angle BAC = \angle DAE = 50^{\circ}$,连接$BD和CE$,将$\triangle ADE绕点A$旋转($\triangle ADE始终在AB$所在直线的右侧范围内旋转),$BD$、$CE$也随之运动.
(1) 如图①,在$\triangle ADE绕点A$旋转过程中,当$AE// BC$时,求$\angle CAD$的度数;15°
(2) 如图②,当点$D恰好是\triangle ABC$的外心时,连接$DC$,判断四边形$ADCE$的形状,并说明理由.菱形

答案：
(1)解:
∵AB = AC，∠BAC = 50°，
∴∠ABC = ∠ACB = $\frac{1}{2}$(180° - 50°) = 65°.
∵AE // BC，
∴∠CAE = ∠ACB = 65°.
∵∠DAE = 50°，
∴∠CAD = ∠CAE - ∠DAE = 65° - 50° = 15°;　
(2)四边形ADCE为菱形，理由:
∵点D为△ABC的外心，
∴AD = BD = CD.
∵∠BAC = ∠DAE，
∴∠BAC - ∠CAD = ∠DAE - ∠CAD，即∠BAD = ∠CAE.在△BAD和△CAE中，$\begin{cases}BA = CA, \\ ∠BAD = ∠CAE, \\ AD = AE,\end{cases}$
∴△BAD ≌ △CAE (SAS).
∴BD = CE. 又
∵AD = AE，
∴AD = AE = CD = CE.
∴四边形ADCE为菱形.