《2025年轻松作业本九年级数学上册苏科版》

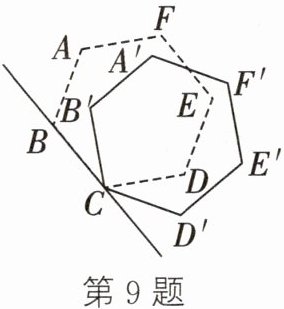
9. 如图,以正六边形ABCDEF的顶点C为旋转中心,按顺时针旋转,使得新正六边形$A'B'CD'E'F'的顶点E'$落在直线BC上,则正六边形ABCDEF至少旋转的度数为90$^{\circ }$.

答案： 90

10. 若一个正六边形的周长为24,则该正六边形的面积为______24√3.

答案： $24\sqrt{3}$

11. 如图,正方形剪去四个角后成为一个正八边形.
(1) 若正八边形的边长为2,则剪去的四个角的面积和为______4;
(2) 若正方形的边长为2,求正八边形的边长.
设正八边形的边长为$y$, 则剪掉的等腰直角三角形的直角边长为$\frac{\sqrt{2}}{2}y. \because$ 正方形的边长为$2, \therefore \frac{\sqrt{2}}{2}y+y+\frac{\sqrt{2}}{2}y=2$, 解得$y=2\sqrt{2}-2. \therefore$ 正八边形的边长为$2\sqrt{2}-2$.

答案：
(1) 4
(2) 设正八边形的边长为$y$, 则剪掉的等腰直角三角形的直角边长为$\frac{\sqrt{2}}{2}y. \because$ 正方形的边长为$2, \therefore \frac{\sqrt{2}}{2}y+y+\frac{\sqrt{2}}{2}y=2$, 解得$y=2\sqrt{2}-2. \therefore$ 正八边形的边长为$2\sqrt{2}-2$.

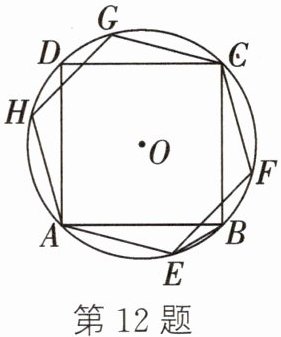
12. 如图,$\odot O$是正方形ABCD与正六边形AEFCGH的外接圆.
(1) 正方形ABCD与正六边形AEFCGH的边长之比为______;
(2) 连接BE,BE是否为$\odot O$的内接正n边形的一边? 如果是,求出n的值;如果不是,请说明理由.

答案：

(1) $\sqrt{2}:1$
(2) 解: $BE$是$\odot O$的内接正十二边形的一边. 理由: 如图, 连接$OA$、$OB$、$OE$, 在正方形$ABCD$中, $\angle AOB=90^{\circ}$, 在正六边形$AEFCGH$中, $\angle AOE=60^{\circ}, \therefore \angle BOE=30^{\circ}. \because n=\frac{360^{\circ}}{30^{\circ}}=12, \therefore BE$是$\odot O$的内接正十二边形的一边.

13. 如图,图①和图②分别是两个相同正方形、正六边形,其中一个正多边形的顶点在另一个正多边形外接圆圆心O处.
(1) 求图①中重叠部分面积与阴影部分面积之比;1:3
(2) 求图②中重叠部分面积与阴影部分面积之比(直接写出答案);1:2
(3) 根据前面的探索和图③,你能否将本题推广到一般的正n边形情况(n为大于2的偶数)? 若能,写出推广问题和结论;若不能,请说明理由.不能. 理由: 正n边形的每一个内角的度数为$\frac{(n - 2)× 180^{\circ}}{n}$, 阴影部分对应的中心角的度数为$360^{\circ}-\frac{(n - 2)× 180^{\circ}}{n}=\frac{180^{\circ}× (n + 2)}{n}$. 两个相同正n边形重叠部分面积与阴影部分面积之比为$\frac{(n - 2)× 180^{\circ}}{n}:\frac{(n + 2)× 180^{\circ}}{n}=(n - 2):(n + 2)$. 但当边数超过6以后, 正多边形的边长小于半径, 因而结论不适合推广.

答案： 解:
(1) 连接$OA$、$OB$, 过点$O$作$OM\perp AB$, 垂足为$M. \because$ 点$O$是正方形$ABCD$外接圆的圆心, $\therefore OA=OB$, $\angle AOB=90^{\circ}. \therefore OM=\frac{1}{2}AB. \therefore S_{\triangle ABO}=\frac{1}{2}AB\cdot OM=\frac{1}{4}AB^{2}=\frac{1}{4}S_{正方形ABCD}. \because$ 易证$\triangle AOF\cong \triangle BOE, \therefore S_{\triangle AOF}=S_{\triangle BOE}. \therefore$ 重叠部分面积$=S_{\triangle BOF}+S_{\triangle BOE}=S_{\triangle BOF}+S_{\triangle AOF}=S_{\triangle ABO}=\frac{1}{4}S_{正方形ABCD}. \therefore S_{阴影}=\frac{3}{4}S_{正方形ABCD}. \therefore$ 重叠部分面积与阴影部分面积之比为$1:3$;
(2) $1:2$
(3) 不能. 理由: 正$n$边形的每一个内角的度数为$\frac{(n - 2)\times 180^{\circ}}{n}$, 阴影部分对应的中心角的度数为$360^{\circ}-\frac{(n - 2)\times 180^{\circ}}{n}=\frac{180^{\circ}\times (n + 2)}{n}$. 两个相同正$n$边形重叠部分面积与阴影部分面积之比为$\frac{(n - 2)\times 180^{\circ}}{n}:\frac{(n + 2)\times 180^{\circ}}{n}=(n - 2):(n + 2)$. 但当边数超过$6$以后, 正多边形的边长小于半径, 因而结论不适合推广.