第10页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
6. 根据你的观察,探究下列问题:
(1) 已知$x^{2}-2xy+2y^{2}+6y+9= 0$,求 xy 的值;
(2) 已知$\triangle ABC$的三边长 a、b、c 都是正整数,且满足$a^{2}+b^{2}-10a-12b+61= 0$,求$\triangle ABC$的最大边 c 的值;
(3) 已知$a-b= 8$,$ab+c^{2}-16c+80= 0$,求$a+b+c$的值.
(1) 已知$x^{2}-2xy+2y^{2}+6y+9= 0$,求 xy 的值;
9
(2) 已知$\triangle ABC$的三边长 a、b、c 都是正整数,且满足$a^{2}+b^{2}-10a-12b+61= 0$,求$\triangle ABC$的最大边 c 的值;
6、7、8、9、10
(3) 已知$a-b= 8$,$ab+c^{2}-16c+80= 0$,求$a+b+c$的值.
8
答案:
解:
(1) $\because x^{2}-2 x y+2 y^{2}+6 y+9=0, \therefore\left(x^{2}-2 x y+\right.$ $y^{2})+\left(y^{2}+6 y+9\right)=0. \therefore(x-y)^{2}+(y+3)^{2}=0. \therefore x-y=$ $0, y+3=0. \therefore x=-3, y=-3. \therefore x y=(-3) \times(-3)=9 ;$
(2) $\because a^{2}+b^{2}-10 a-12 b+61=0, \therefore\left(a^{2}-10 a+25\right)+\left(b^{2}-\right.$ $12 b+36)=0. \therefore(a-5)^{2}+(b-6)^{2}=0. \therefore a-5=0, b-6=0.$ $\therefore a=5, b=6. \because 6-5<c<6+5, c \geqslant 6, \therefore 6 \leqslant c<11.$ $\therefore \triangle ABC$ 的最大边 $c$ 的值可能是 $6 、 7 、 8 、 9 、 10$;
(3) $\because a-$ $b=8, a b+c^{2}-16 c+80=0, \therefore a(a-8)+16+(c-8)^{2}=0$. $\therefore(a-4)^{2}+(c-8)^{2}=0. \therefore a-4=0, c-8=0. \therefore a=4, c=8$, 即 $b=a-8=4-8=-4. \therefore a+b+c=4-4+8=8$.
(1) $\because x^{2}-2 x y+2 y^{2}+6 y+9=0, \therefore\left(x^{2}-2 x y+\right.$ $y^{2})+\left(y^{2}+6 y+9\right)=0. \therefore(x-y)^{2}+(y+3)^{2}=0. \therefore x-y=$ $0, y+3=0. \therefore x=-3, y=-3. \therefore x y=(-3) \times(-3)=9 ;$
(2) $\because a^{2}+b^{2}-10 a-12 b+61=0, \therefore\left(a^{2}-10 a+25\right)+\left(b^{2}-\right.$ $12 b+36)=0. \therefore(a-5)^{2}+(b-6)^{2}=0. \therefore a-5=0, b-6=0.$ $\therefore a=5, b=6. \because 6-5<c<6+5, c \geqslant 6, \therefore 6 \leqslant c<11.$ $\therefore \triangle ABC$ 的最大边 $c$ 的值可能是 $6 、 7 、 8 、 9 、 10$;
(3) $\because a-$ $b=8, a b+c^{2}-16 c+80=0, \therefore a(a-8)+16+(c-8)^{2}=0$. $\therefore(a-4)^{2}+(c-8)^{2}=0. \therefore a-4=0, c-8=0. \therefore a=4, c=8$, 即 $b=a-8=4-8=-4. \therefore a+b+c=4-4+8=8$.
7. 已知 a、b 满足等式$x= a^{2}-6ab+9b^{2}$,$y= 4a-12b-4$,则 x、y 的大小关系是 (
A. $x= y$
B. $x>y$
C. $x<y$
D. $x≥y$
D
)A. $x= y$
B. $x>y$
C. $x<y$
D. $x≥y$
答案:
D
8. 阅读下列材料:
利用完全平方公式,将多项式$x^{2}+bx+c$变形为$(x+m)^{2}+n$的形式.
例如:$x^{2}-8x+17= x^{2}-2\cdot x\cdot 4+4^{2}-4^{2}+17= (x-4)^{2}+1$.
(1) 填空:将多项式$x^{2}-2x+3$变形为$(x+m)^{2}+n$的形式,并判断$x^{2}-2x+3$与 0 的大小关系.
$\because x^{2}-2x+3= (x-$
$\therefore x^{2}-2x+3$
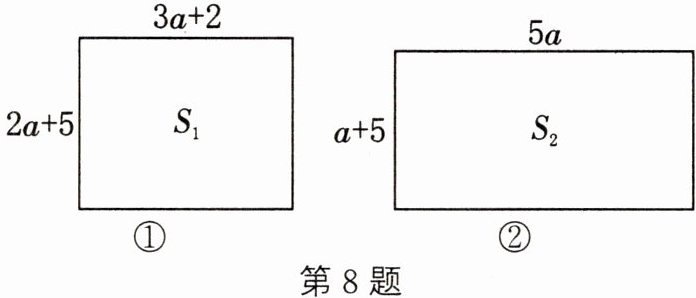
(2) 如图①所示的矩形边长分别是$2a+5$、$3a+2$,求矩形的面积$S_{1}$(用含 a 的式子表示);
如图②所示的矩形边长分别是 5a、$a+5$,求矩形的面积$S_{2}$(用含 a 的式子表示);
(3) 比较(2)中$S_{1}与S_{2}$的大小,并说明理由.
利用完全平方公式,将多项式$x^{2}+bx+c$变形为$(x+m)^{2}+n$的形式.
例如:$x^{2}-8x+17= x^{2}-2\cdot x\cdot 4+4^{2}-4^{2}+17= (x-4)^{2}+1$.
(1) 填空:将多项式$x^{2}-2x+3$变形为$(x+m)^{2}+n$的形式,并判断$x^{2}-2x+3$与 0 的大小关系.
$\because x^{2}-2x+3= (x-$
1
$)^{2}+$2
,$\therefore x^{2}-2x+3$
>
0(填“>”“<”或“=”).(2) 如图①所示的矩形边长分别是$2a+5$、$3a+2$,求矩形的面积$S_{1}$(用含 a 的式子表示);
如图②所示的矩形边长分别是 5a、$a+5$,求矩形的面积$S_{2}$(用含 a 的式子表示);
(3) 比较(2)中$S_{1}与S_{2}$的大小,并说明理由.

答案:
解:
(1) 1 2 $>$
(2) $S_{1}=(2 a+5)(3 a+2)=6 a^{2}+19 a+$ $10, S_{2}=5 a(a+5)=5 a^{2}+25 a$;
(3) $S_{1}>S_{2}$ 理由: $S_{1}-$ $S_{2}=6 a^{2}+19 a+10-\left(5 a^{2}+25 a\right)=a^{2}-6 a+10=(a-3)^{2}+1$, $\because(a-3)^{2} \geqslant 0, \therefore(a-3)^{2}+1>0. \therefore S_{1}-S_{2}>0. \therefore S_{1}>S_{2}$.
(1) 1 2 $>$
(2) $S_{1}=(2 a+5)(3 a+2)=6 a^{2}+19 a+$ $10, S_{2}=5 a(a+5)=5 a^{2}+25 a$;
(3) $S_{1}>S_{2}$ 理由: $S_{1}-$ $S_{2}=6 a^{2}+19 a+10-\left(5 a^{2}+25 a\right)=a^{2}-6 a+10=(a-3)^{2}+1$, $\because(a-3)^{2} \geqslant 0, \therefore(a-3)^{2}+1>0. \therefore S_{1}-S_{2}>0. \therefore S_{1}>S_{2}$.
查看更多完整答案,请扫码查看


