第84页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
9. 某居民小区为了了解本小区100户居民家庭平均每月使用塑料袋的数量情况,随机调查了10户居民家庭每月使用塑料袋的数量,结果如下(单位:只):65,70,85,74,86,78,74,92,82,94.根据统计情况,利用计算器估计该小区这100户居民家庭平均每月使用塑料袋共为
8000
只。
答案:
8000
10. 某单位招聘员工,采取笔试与面试结合的方式进行,两项成绩的原始分均为100分。前3名选手的得分如下表:

根据规定,笔试成绩和面试成绩分别按一定的百分比折合成综合成绩(综合成绩的满分仍为100分)。
(1)现得知1号选手的综合成绩为88分,求笔试成绩和面试成绩各占的百分比;
笔试成绩占的百分比为
(2)求出其余两名选手的综合成绩,并以综合成绩排序确定前两名人选。
2号选手的综合成绩为

根据规定,笔试成绩和面试成绩分别按一定的百分比折合成综合成绩(综合成绩的满分仍为100分)。
(1)现得知1号选手的综合成绩为88分,求笔试成绩和面试成绩各占的百分比;
笔试成绩占的百分比为
40%
,面试成绩占的百分比为60%
;(2)求出其余两名选手的综合成绩,并以综合成绩排序确定前两名人选。
2号选手的综合成绩为
89.6
分,3号选手的综合成绩为85.2
分,综合成绩排序确定前两名人选是2号和1号
。
答案:
解:
(1)设笔试成绩占的百分比为x,则面试成绩占的百分比为$(1 - x)$,根据题意,得$85x + 90(1 - x) = 88$,解得$x = 0.4 = 40\%$,
∴$1 - x = 1 - 40\% = 60\%$。答:笔试成绩占的百分比为40%,面试成绩占的百分比为60%;
(2)2号选手的综合成绩为$92×40\% + 88×60\% = 89.6$(分)。3号选手的综合成绩为$84×40\% + 86×60\% = 85.2$(分)。答:综合成绩排序确定前两名人选是2号和1号。
(1)设笔试成绩占的百分比为x,则面试成绩占的百分比为$(1 - x)$,根据题意,得$85x + 90(1 - x) = 88$,解得$x = 0.4 = 40\%$,
∴$1 - x = 1 - 40\% = 60\%$。答:笔试成绩占的百分比为40%,面试成绩占的百分比为60%;
(2)2号选手的综合成绩为$92×40\% + 88×60\% = 89.6$(分)。3号选手的综合成绩为$84×40\% + 86×60\% = 85.2$(分)。答:综合成绩排序确定前两名人选是2号和1号。
11. 为了解某校八年级男生在体能测试中引体向上项目的情况,随机抽查了部分男生引体向上项目的测试成绩,绘制出统计图如图所示,请根据相关信息,解答下列问题:
(1)本次接受随机抽样调查的男生人数为______
(2)求本次调查获取的样本数据的平均数、众数、中位数;
(3)若规定引体向上6次及以上为该项目良好,根据样本数据,估计该校320名男生中该项目良好的人数;
(4)根据良好人数,为了中招体育测试能有更多人得到高分,请你给该校男生提出一些相关建议(最少两条)。
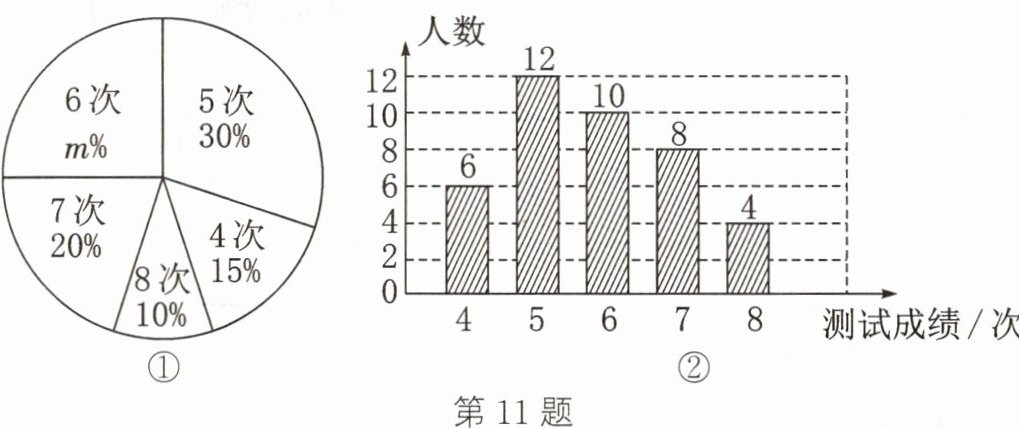
(1)本次接受随机抽样调查的男生人数为______
40
,图①中m的值为______25
;(2)求本次调查获取的样本数据的平均数、众数、中位数;
(3)若规定引体向上6次及以上为该项目良好,根据样本数据,估计该校320名男生中该项目良好的人数;
(4)根据良好人数,为了中招体育测试能有更多人得到高分,请你给该校男生提出一些相关建议(最少两条)。

答案:
(1)40 25
(2)平均数为$\frac{4×6 + 5×12 + 6×10 + 7×8 + 8×4}{40} = 5.8$(次),这40名男生引体向上的次数出现最多的是5次,共出现12次,因此众数是5,将这40名男生引体向上的次数从小到大排列后,处在中间位置的两个数的平均数是$\frac{6 + 6}{2} = 6$(次),因此中位数是6;
(3)$320×\frac{10 + 8 + 4}{40} = 176$(人)。答:该校320名男生中该项目良好的人数大约为176;
(4)答案不唯一,如加强对“5次”男生的训练,使其进入“良好”行列;每名男生均要积极训练力争取得更加优异的成绩。
![img alt=14]
(1)40 25
(2)平均数为$\frac{4×6 + 5×12 + 6×10 + 7×8 + 8×4}{40} = 5.8$(次),这40名男生引体向上的次数出现最多的是5次,共出现12次,因此众数是5,将这40名男生引体向上的次数从小到大排列后,处在中间位置的两个数的平均数是$\frac{6 + 6}{2} = 6$(次),因此中位数是6;
(3)$320×\frac{10 + 8 + 4}{40} = 176$(人)。答:该校320名男生中该项目良好的人数大约为176;
(4)答案不唯一,如加强对“5次”男生的训练,使其进入“良好”行列;每名男生均要积极训练力争取得更加优异的成绩。
![img alt=14]
查看更多完整答案,请扫码查看


