《2025年5年中考3年模拟数学广东专版》

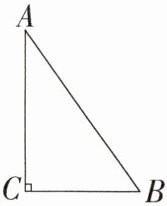
6. (2020 广州,7,3 分)如图,Rt△ABC 中,∠C = 90°,AB = 5,cos A = $\frac{4}{5}$,以点 B 为圆心,r 为半径作⊙B,当 r = 3 时,⊙B 与 AC 的位置关系是　　　　(　　　)
　　　　　　　　　　　　　　
　
A. 相离　　　　　　　B. 相切
　
C. 相交　　　　　　　D. 无法确定

答案： B
∵∠C =90°,AB =5,cos A =$\frac{AC}{AB}$=$\frac{4}{5}$,
∴AC =AB·cos A =5×$\frac{4}{5}$=4,
∴BC =$\sqrt{AB^{2}-AC^{2}}$=$\sqrt{5^{2}-4^{2}}$=3.
∵r =3,
∴⊙B与AC的位置关系是相切.

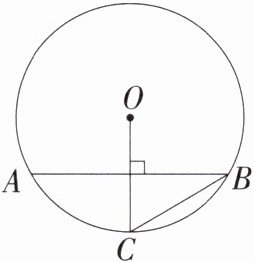
7. (2024 广州,9,3 分)如图,⊙O 中,弦 AB 的长为 4$\sqrt{3}$,点 C 在⊙O 上,OC⊥AB,∠ABC = 30°.⊙O 所在的平面内有一点 P,若 OP = 5,则点 P 与⊙O 的位置关系是　　　　　　　　(　　　)
　　　　　　
　
A. 点 P 在⊙O 上　　B. 点 P 在⊙O 内
　
C. 点 P 在⊙O 外　　D. 无法确定

答案：
C 如图,连接OA,设OC与AB的交点为D,

∵OC为半径,且OC⊥AB,
∴AD =$\frac{1}{2}$AB =2$\sqrt{3}$,
∵∠ABC =30°,
∴∠AOC =2∠ABC =60°.
在Rt△ADO中,sin∠AOD =$\frac{AD}{OA}$,
∴OA =$\frac{AD}{\sin60^{\circ}}=\frac{2\sqrt{3}}{\frac{\sqrt{3}}{2}}$=4,即⊙O的半径为4.
∵OP =5＞4,
∴点P在⊙O外.

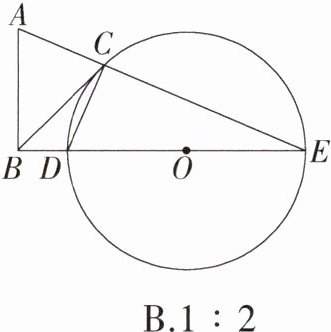
8. (2022 深圳,10,3 分)已知三角形 ABE 为直角三角形,∠ABE = 90°,BC 为圆 O 切线,C 为切点,CA = CD,则△ABC 和△CDE 面积之比为　　　　　　　　　　　　　　　(　　　)
　　　　　　
　

A. 1 : 3
B. 1 : 2
C. $\sqrt{2}$ : 2　　　　　
　D. ($\sqrt{2}$ - 1) : 1

答案：
B 如图,连接OC,
∵BC是⊙O的切线,OC为半径,
∴OC⊥BC,即∠OCB =90°,
∴∠COD+∠OBC =90°,
∵∠ABE =90°,
∴∠ABC+∠OBC =90°,
∴∠ABC =∠COD,
∵DE是⊙O的直径,
∴∠DCE =90°,即∠OCE+∠OCD =90°,
又∠A+∠E =90°,而∠E =∠OCE,
∴∠A =∠OCD,又
∵AC =CD,
∴△ABC≌△COD,
∵EO =DO,
∴S△COD =S△COE =$\frac{1}{2}$S△CDE,
∴S△ABC =$\frac{1}{2}$S△CDE,即△ABC和△CDE面积之比为1∶2.

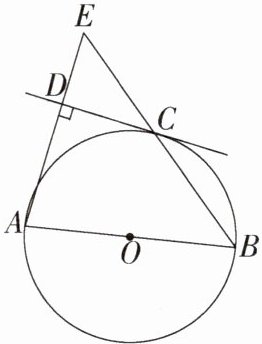
9. (2020 深圳,20,8 分)如图,AB 为⊙O 的直径,点 C 在⊙O 上,AD 与过点 C 的切线互相垂直，垂足为 D,连接 BC 并延长,交 AD 的延长线于点 E.
(1)求证:AE = AB;
　(2)若 AB = 10,BC = 6,求 CD 的长.
　　　　　　　　　　　　

答案： 解析
(1)证明:连接AC、OC.
∵CD⊥AE,
∴∠CDE =90°.
又
∵CD为⊙O的切线,
∴∠OCD =90° =∠CDE,
∴CO//AE.
∵O为AB的中点,
∴CO为△BAE的中位线,
∴CO =$\frac{1}{2}$AE.
∵AB为⊙O的直径,
∴∠ACB =90°.
在Rt△ABC中,
∵CO为斜边中线,
∴CO =$\frac{1}{2}$AB,
∴AE =AB.
(2)
∵AB =10,BC =6,
∴AE =AB =10,CE =CB =6,AC =$\sqrt{AB^{2}-BC^{2}}$=8.
∵S△ACE =$\frac{1}{2}$AC·CE =$\frac{1}{2}$AE·CD,
∴8×6 =10CD,
∴CD =$\frac{24}{5}$.

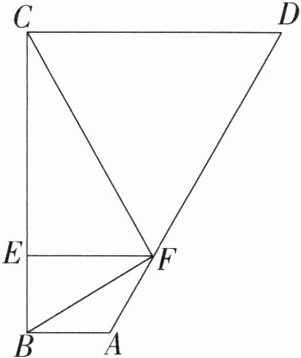
10. (2021 广东,24,10 分)如图,在四边形 ABCD 中,AB//CD,AB≠CD,∠ABC = 90°,点 E、F 分别在线段 BC、AD 上,且 EF//CD,AB = AF,CD = DF;
　(1)求证:CF⊥FB;
　(2)求证:以 AD 为直径的圆与 BC 相切;
　(3)若 EF = 2,∠DFE = 120°,求△ADE 的面积.
　　　　　　　　　　　

答案：
解析
(1)证明:
∵AB =AF,
∴∠ABF =∠AFB.
∵CD =DF,
∴∠DCF =∠DFC.
∵CD//EF,
∴∠DCF =∠CFE.
∴∠CFE =∠DFC.
又
∵AB//CD,EF//CD,
∴AB//EF.
∴∠EFB =∠FBA,
∴∠EFB =∠AFB.
∵∠DFC+∠CFE+∠EFB+∠AFB =180°,
∴∠CFE+∠BFE =90°,即∠CFB =90°.
∴CF⊥FB.
(2)证明:取AD的中点O,过点O作OG⊥CB于点G,连接CA交OG于点H.

∵OG⊥BC,∠ABC =∠BCD =90°,
∴OG//CD.
∵AO =DO,
∴AH =CH,CG =BG.
∴GH是△ABC的中位线,
∴GH =$\frac{1}{2}$AB.同理可得OH =$\frac{1}{2}$CD.
∴OG =GH +HO =$\frac{1}{2}$(AB +CD)=$\frac{1}{2}$(AF +FD)=$\frac{1}{2}$AD =OD.
∵OD是半径,
∴以AD为直径的圆与BC相切.
(3)连接DE、AE.
∵∠DFE =120°,由
(1)得∠DFC =∠CFE,
∴∠DFC =∠CFE =$\frac{1}{2}$∠DFE =60°.
由
(1)得EF//AB,∠ABC =90°,
∴∠CEF =∠ABC =90°.
∴∠BEF =90°,∠EFB =30°.
在Rt△CEF中,CE =EF·tan 60° =2$\sqrt{3}$.在Rt△EFB中,EB =EF·tan 30°=$\frac{2\sqrt{3}}{3}$.
∴S△ADE =S△DEF +S△AFE =$\frac{1}{2}$EF·CE+$\frac{1}{2}$EF·EB =$\frac{1}{2}$×2×2$\sqrt{3}$+$\frac{1}{2}$×2×$\frac{2\sqrt{3}}{3}$=$\frac{8\sqrt{3}}{3}$.