《2025年5年中考3年模拟数学广东专版》

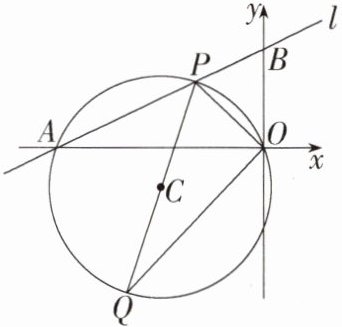
7.(2021广州,23,10分)如图,在平面直角坐标系xOy中,直线l:y = $\frac{1}{2}$x + 4分别与x轴,y轴相交于A,B两点,点P(x,y)为直线l在第二象限的点.
　(1)求A,B两点的坐标;
　(2)设△PAO的面积为S,求S关于x的函数解析式,并写出x的取值范围;
　(3)作△PAO的外接圆⊙C,延长PC交⊙C于点Q,当△POQ的面积最小时,求⊙C的半径.
　　　　　　　　　　　

答案：
5年中考
7.解析
(1)令y = $\frac{1}{2}$x + 4中x = 0,则y = 4.
∴ 点B的坐标为(0,4).
令y = $\frac{1}{2}$x + 4中y = 0,则x = -8.
∴ 点A的坐标为(-8,0).
(2)
∵ 点P(x,y)在直线l上,
∴ y = $\frac{1}{2}$x + 4.
∴ S = $\frac{1}{2}$·OA·($\frac{1}{2}$x + 4)=$\frac{1}{2}$×8×($\frac{1}{2}$x + 4)= 2x + 16.
∵ 点P在第二象限,
∴ -8 ＜ x ＜ 0.
∴ S = 2x + 16(-8 ＜ x ＜ 0).
(3)依题意,OB = 4,OA = 8,点C为△PAO外接圆圆心.作OA的中垂线l',连接OC.
∴ 点C在OA的中垂线l'上.
∵ PQ为直径,
∴ ∠POQ = 90° = ∠BOA.
又
∵ ∠Q = ∠BAO,
∴ △QOP∽△AOB.
∴ OP : OQ : PQ = OB : OA : BA = 1 : 2 : $\sqrt{5}$.
∴ △POQ的面积最小,即PQ的值最小,即半径OC的值最小.
设直线l'与OA相交于点C₁.
∴ 当OC = OC₁时,半径OC最小,
半径最小值为4.故当△POQ的面积最小时,⊙C的半径为4.

8.(2024广州,23,10分)一个人的脚印信息往往对应着这个人某些方面的基本特征.某数学兴趣小组收集了大量不同人群的身高和脚长数据,通过对数据的整理和分析,发现身高y和脚长x之间近似存在一个函数关系,部分数据如下表:
　
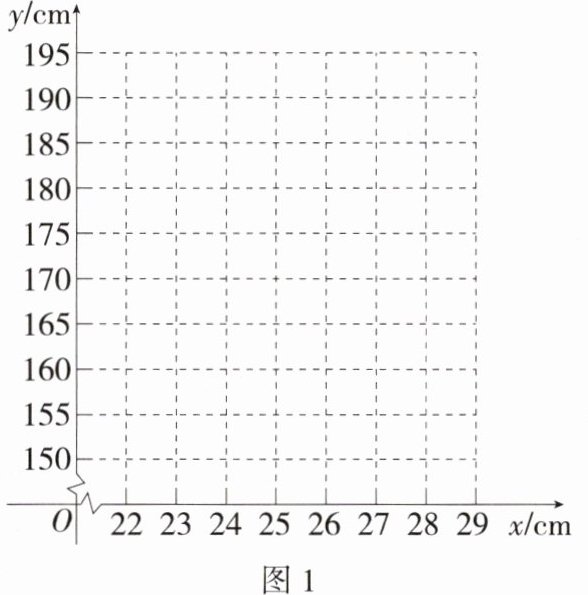
　(1)在图1中描出表中数据对应的点(x,y);
　(2)根据表中数据,从y = ax + b(a≠0)和y = $\frac{k}{x}$(k≠0)中选择一个函数模型,使它能近似地反映身高和脚长的函数关系,并求出这个函数的解析式(不要求写出x的取值范围);
　(3)如图2,某场所发现了一个人的脚印,脚长约为25.8cm,请根据(2)中求出的函数解析式,估计这个人的身高.
　　

答案：
8.解析
(1)如图所示.

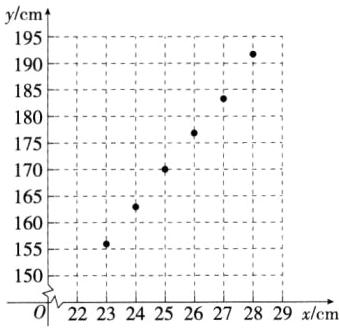
(2)由
(1)知应选择函数y = ax + b(a≠0)近似地反映身高和脚长的函数关系.
将(23,156),(24,163)代入得$\begin{cases}23a + b = 156,\\24a + b = 163,\end{cases}$解得$\begin{cases}a = 7,\\b = -5,\end{cases}$
∴ 一次函数解析式为y = 7x - 5.
(3)将x = 25.8代入y = 7x - 5得y = 7×25.8 - 5 = 175.6.
∴ 估计这个人的身高为175.6 cm.