《2025年5年中考3年模拟数学广东专版》

1. (2021 广州,9,3 分)如图,在 Rt△ABC 中,∠C = 90°,AC = 6,BC = 8,将△ABC 绕点 A 逆时针旋转得到△AB'C',使点 C'落在 AB 边上,连接 BB',则 sin∠BB'C'的值为 ( )

A.$\frac{3}{5}$
B.$\frac{4}{5}$
C.$\frac{\sqrt{5}}{5}$
D.$\frac{2\sqrt{5}}{5}$

答案： C
∵∠C=90°,AC=6,BC=8,
∴AB=$\sqrt{AC^{2}+BC^{2}}=\sqrt{6^{2}+8^{2}}$=10.
∵∠AC'B'=90°,AC'=AC=6,B'C'=BC=8,
∴∠B'C'B=90°,C'B=4.
∴在Rt△B'C'B中,B'B=$\sqrt{C'B'^{2}+C'B^{2}}=\sqrt{8^{2}+4^{2}}$=4√5.
∴sin∠BB'C'=$\frac{C'B}{B'B}=\frac{4}{4\sqrt{5}}=\frac{\sqrt{5}}{5}$

2. (2022 广东,11,3 分)sin 30° = ________.

答案： 答案　$\frac{1}{2}$

3. (2021 广东,16,4 分)如图,在▱ABCD 中,AD = 5,AB = 12,sin A = $\frac{4}{5}$.过点 D 作 DE⊥AB,垂足为 E,则 sin∠BCE = ________.

答案：
答案　$\frac{9\sqrt{10}}{50}$
解析　过点C作CF⊥AB,交AB的延长线于点F.

∵四边形ABCD为平行四边形，
∴易证△BCF≌△ADE,
∴CF=DE,BF=AE.
在Rt△ADE中,sinA=$\frac{DE}{AD}=\frac{DE}{5}=\frac{4}{5}$，
∴DE=4,
∴AE=$\sqrt{AD^{2}-DE^{2}}$=3,
∴CF=4,BF=3,BC=5.
∵AB=12,
∴BE=9,
∴EF=12.
在Rt△ECF中,EC=$\sqrt{CF^{2}+EF^{2}}=\sqrt{4^{2}+12^{2}}$=4$\sqrt{10}$.过点B作BH⊥EC于点H.
∵$S_{\triangle EBC}=\frac{1}{2}EB\cdot CF=\frac{1}{2}EC\cdot BH$，
∴BH=$\frac{EB\cdot CF}{EC}=\frac{9\times4}{4\sqrt{10}}=\frac{9\sqrt{10}}{10}$，
∴sin∠BCE=$\frac{BH}{BC}=\frac{\frac{9\sqrt{10}}{10}}{5}=\frac{9\sqrt{10}}{50}$

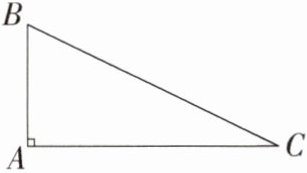
4. (2021 广东,20,6 分)如图,在 Rt△ABC 中,∠A = 90°.作 BC 的垂直平分线交 AC 于点 D,延长 AC 至点 E,使 CE = AB.
(1)若 AE = 1,求△ABD 的周长;
(2)若 AD = $\frac{1}{3}$BD,求 tan∠ABC 的值.

答案：
解析　
(1)
∵点D在线段BC的垂直平分线上，
∴DB=DC.
又CE=AB,
∴△ABD的周长=AD+DB+BA=AD+DC+CE=AE=1.
∴△ABD的周长为1.

(2)设AD=x.
∵AD=$\frac{1}{3}BD$，
∴BD=CD=3x.
∴AC=AD+DC=x+3x=4x.
在Rt△ABD中,AB=$\sqrt{BD^{2}-AD^{2}}$=2√2x.在Rt△ABC中,tan∠ABC=$\frac{AC}{AB}=\frac{4x}{2\sqrt{2}x}=\sqrt{2}$

5. (2023 深圳,9,3 分)爬坡时坡面与水平面的夹角(坡角)为α,则每爬 1 m 耗能(1.025 - cos α)J,若某人爬了 1 000 m,该坡角为 30°,则他耗能(参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414) ( )
A.58 J
B.159 J
C.1 025 J
D.1 732 J

答案： B　由题意得1000×(1.025 - cos 30°)= 1000×$(1.025-\frac{\sqrt{3}}{2})$≈159(J).

6. (2020 深圳,16,3 分)如图,在四边形 ABCD 中,AC 与 BD 相交于点 O,∠ABC = ∠DAC = 90°,tan∠ACB = $\frac{1}{2}$,$\frac{BO}{OD}$ = $\frac{4}{3}$,则$\frac{S_{\triangle ABD}}{S_{\triangle CBD}}$ = ________.

答案：
答案　$\frac{3}{32}$
解析　如图，延长DA交CB的延长线于E.

∵CA⊥DE,
∴∠CAE=90°,
∴∠EAB+∠CAB=90°.
∵∠ABC=90°,
∴∠BAC+∠BCA=90°,
∴∠EAB=∠ACB.
∵tan∠ACB=$\frac{1}{2}$,
∴tan∠BAE=$\frac{1}{2}$.
设BE=m,则BA=2m,BC=4m.
在Rt△ABE中,由勾股定理可得AE=$\sqrt{BE^{2}+AB^{2}}=\sqrt{5}m$
在Rt△ABC中，由勾股定理可得AC=$\sqrt{AB^{2}+BC^{2}}$=2√5m.
∵$\frac{BO}{OD}=\frac{4}{3}$，△ADO与△ABO分别以OD、BO为底则同高，△DOC与△BOC同理，
∴$\frac{S_{\triangle ABO}}{S_{\triangle ADO}}=\frac{S_{\triangle BOC}}{S_{\triangle DOC}}=\frac{4}{3}$，
∴$\frac{S_{\triangle ABO}+S_{\triangle BOC}}{S_{\triangle ADO}+S_{\triangle DOC}}=\frac{S_{\triangle ABC}}{S_{\triangle ADC}}=\frac{4}{3}$.
∵$S_{\triangle ABC}=\frac{1}{2}AB\cdot BC = 4m^{2}$，$S_{\triangle ADC}=\frac{1}{2}AD\cdot AC=\sqrt{5}m\cdot AD$，
∴$\frac{4m^{2}}{\sqrt{5}m\cdot AD}=\frac{4}{3}$，
∴AD=$\frac{3}{\sqrt{5}}m$.
∴$\frac{AD}{AE}=\frac{\frac{3}{\sqrt{5}}m}{\sqrt{5}m}=\frac{3}{5}$，
∴$\frac{AD}{AE + AD}=\frac{AD}{DE}=\frac{3}{5 + 3}=\frac{3}{8}$.
∵△ABD与△DEB分别以AD和DE为底则同高，
∴$\frac{S_{\triangle ABD}}{S_{\triangle DEB}}=\frac{3}{8}$，
∴$S_{\triangle ABD}=\frac{3}{8}S_{\triangle DEB}$.
∵△DBE与△DBC分别以BE和BC为底则同高，
∴$\frac{S_{\triangle DBE}}{S_{\triangle DBC}}=\frac{BE}{BC}=\frac{m}{4m}=\frac{1}{4}$，
∴$S_{\triangle DBE}=\frac{1}{4}S_{\triangle DBC}$，
∴$S_{\triangle ABD}=\frac{3}{8}S_{\triangle DEB}=\frac{3}{8}\times\frac{1}{4}S_{\triangle DBC}=\frac{3}{32}S_{\triangle DBC}$，
∴$\frac{S_{\triangle ABD}}{S_{\triangle CBD}}=\frac{3}{32}$.

7. (2023 广东,18,7 分)2023 年 5 月 30 日,神舟十六号载人飞船发射取得圆满成功,3 名航天员顺利进驻中国空间站.图中的照片展示了中国空间站上机械臂的一种工作状态.当两臂 AC = BC = 10 m,两臂夹角∠ACB = 100°时,求 A,B 两点间的距离.(结果精确到 0.1 m,参考数据:sin 50°≈0.766,cos 50°≈0.643,tan 50°≈1.192)

答案：
解析　连接AB,过点C作CD⊥AB,垂足为D.

∵AC=BC,∠ACB=100°,
∴∠ACD=$\frac{1}{2}$∠ACB=50°.
在Rt△ADC中，
∵sin∠ACD=$\frac{AD}{AC}$，
∴AD=AC·sin∠ACD=10×sin50°≈7.66(m).
∴AB=2AD≈15.3(m).
答:A,B两点间的距离约为15.3m.