第105页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
7.(2020深圳,2,3分)下列图形既是轴对称图形又是中心对称图形的是 ( )


答案:
B
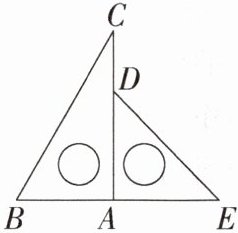
8.(2019广州,14,3分)一副三角板如图放置,将三角板ADE绕点A逆时针旋转α(0°<α<90°),使得三角板ADE的一边所在的直线与BC垂直,则α 的度数为__________.

答案:
答案 15°或60°
解析 ①当DE⊥BC时,如图,设DE与AC交于点F,

∵∠AFE=∠CFD=90°-∠C=90°-30°=60°,
∴∠FAE=180°-∠AFE-∠E=180°-60°-45°=75°,
∴∠DAC=∠DAE-∠FAE=90°-75°=15°,
∴α=15°.
②当AD⊥BC时,如图,设DE与AC交于点F,

∵∠C=30°,AD⊥BC,
∴∠DAC=90°-∠C=60°,
∴α=60°.
综上所述,α的度数为15°或60°.
答案 15°或60°
解析 ①当DE⊥BC时,如图,设DE与AC交于点F,

∵∠AFE=∠CFD=90°-∠C=90°-30°=60°,
∴∠FAE=180°-∠AFE-∠E=180°-60°-45°=75°,
∴∠DAC=∠DAE-∠FAE=90°-75°=15°,
∴α=15°.
②当AD⊥BC时,如图,设DE与AC交于点F,

∵∠C=30°,AD⊥BC,
∴∠DAC=90°-∠C=60°,
∴α=60°.
综上所述,α的度数为15°或60°.
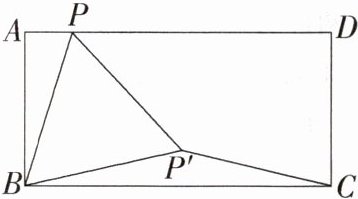
9.(2022广州,16,3分)如图,在矩形ABCD中,BC = 2AB,点P为边AD上的一个动点,线段BP绕点B顺时针旋转60°得到线段BP',连接PP',CP'.
当点P'落在边BC上时,∠PP'C的度数为__________;
当线段CP'的长度最小时,∠PP'C的度数为__________.
当点P'落在边BC上时,∠PP'C的度数为__________;
当线段CP'的长度最小时,∠PP'C的度数为__________.

答案:
答案 120°;75°
解析 当点P'落在边BC上时,B,P',C三点共线,
∵BP=BP',∠PBP'=60°,
∴△BPP'为等边三角形,
∴∠BP'P=60°,
∴∠PP'C=120°.
将线段AD绕点B顺时针旋转60°得到线段A'D',易知线段A'D'为点P'的运动轨迹,设A'D'与BC交于点E.连接A'B,易知∠A'EB=60°.

当CP'⊥A'D'时,CP'取最小值.
易证△ABP≌△A'BP',
∴∠A=∠A'=90°,
∴A'B//CP',
∴∠P'CE=∠A'BE=30°.
设AB=A'B=a,则BC=2a,$A'E=\frac{\sqrt{3}}{3}a,$$BE=\frac{2\sqrt{3}}{3}a,$
∴$CE=2a-\frac{2\sqrt{3}}{3}a,$
∴$EP'=a-\frac{\sqrt{3}}{3}a.$
∴A'P'=A'E+EP'=a,
∴A'B=A'P',
∴∠A'P'B=45°,又
∵△BPP'为等边三角形,
∴∠A'P'P=15°,
∴∠PP'C=90°-15°=75°.
答案 120°;75°
解析 当点P'落在边BC上时,B,P',C三点共线,
∵BP=BP',∠PBP'=60°,
∴△BPP'为等边三角形,
∴∠BP'P=60°,
∴∠PP'C=120°.
将线段AD绕点B顺时针旋转60°得到线段A'D',易知线段A'D'为点P'的运动轨迹,设A'D'与BC交于点E.连接A'B,易知∠A'EB=60°.

当CP'⊥A'D'时,CP'取最小值.
易证△ABP≌△A'BP',
∴∠A=∠A'=90°,
∴A'B//CP',
∴∠P'CE=∠A'BE=30°.
设AB=A'B=a,则BC=2a,$A'E=\frac{\sqrt{3}}{3}a,$$BE=\frac{2\sqrt{3}}{3}a,$
∴$CE=2a-\frac{2\sqrt{3}}{3}a,$
∴$EP'=a-\frac{\sqrt{3}}{3}a.$
∴A'P'=A'E+EP'=a,
∴A'B=A'P',
∴∠A'P'B=45°,又
∵△BPP'为等边三角形,
∴∠A'P'P=15°,
∴∠PP'C=90°-15°=75°.
10.(2020深圳,22,9分)背景:一次小组合作探究课上,小明将两个正方形按如图所示的位置摆放(点E、A、D在同一条直线上),发现BE = DG且BE⊥DG.
小组讨论后,提出了下列三个问题,请你帮助解答.
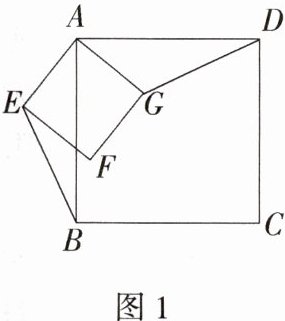
(1)将正方形AEFG绕点A按逆时针方向旋转(如图1),还能得到BE = DG吗?若能,请给出证明,若不能,请说明理由.
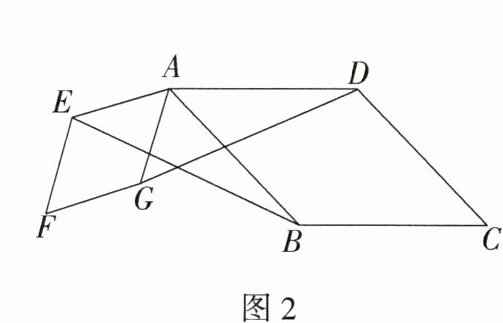
(2)把背景中的正方形分别改成菱形AEFG 和菱形ABCD,将菱形AEFG绕点A按顺时针方向旋转(如图2),试问当∠EAG与∠BAD 的大小满足怎样的关系时,背景中的结论BE = DG仍成立?请说明理由.
(3)把背景中的正方形分别改成矩形AEFG 和矩形ABCD,且$\frac{AE}{AG}=\frac{AB}{AD}=\frac{2}{3}$,AE = 4,AB = 8,将矩形AEFG绕点A按顺时针方向旋转(如图3),连接DE,BG.小组发现:在旋转过程中,DE²+BG²的值是定值,请求出这个定值.


小组讨论后,提出了下列三个问题,请你帮助解答.
(1)将正方形AEFG绕点A按逆时针方向旋转(如图1),还能得到BE = DG吗?若能,请给出证明,若不能,请说明理由.
(2)把背景中的正方形分别改成菱形AEFG 和菱形ABCD,将菱形AEFG绕点A按顺时针方向旋转(如图2),试问当∠EAG与∠BAD 的大小满足怎样的关系时,背景中的结论BE = DG仍成立?请说明理由.
(3)把背景中的正方形分别改成矩形AEFG 和矩形ABCD,且$\frac{AE}{AG}=\frac{AB}{AD}=\frac{2}{3}$,AE = 4,AB = 8,将矩形AEFG绕点A按顺时针方向旋转(如图3),连接DE,BG.小组发现:在旋转过程中,DE²+BG²的值是定值,请求出这个定值.




答案:
解析
(1)能.
证明如下:
∵四边形AEFG为正方形,
∴AE=AG,∠EAG=90°.
∵四边形ABCD为正方形,
∴AB=AD,∠BAD=90°,
∴∠EAB=∠GAD.
∴△AEB≌△AGD(SAS),
∴BE=DG.
(2)当∠EAG=∠BAD时,BE=DG.
理由如下:
∵∠EAG=∠BAD,
∴∠EAB=∠GAD.
∵四边形AEFG和四边形ABCD均为菱形,
∴AE=AG,AB=AD.
∴△AEB≌△AGD(SAS),
∴BE=DG.
(3)过E作EM⊥DA的延长线于点M,过G作GN⊥AB于点N.
∵$\frac{AE}{AG}=\frac{AB}{AD}=\frac{2}{3},$AE=4,AB=8,
∴AG=6,AD=12.
∵∠EAG=∠MAN=90°,
∴∠MAE=∠NAG.
又
∵∠AME=∠ANG,
∴△AME∽△ANG,
∴$\frac{ME}{NG}=\frac{AM}{AN}=\frac{AE}{AG}=\frac{2}{3}.$设EM=2a,AM=2b,
则GN=3a,AN=3b,$4a^{2}+4b^{2}=16,$
∴BN=8 - 3b,$a^{2}+b^{2}=4,$
∴$ED^{2}=(2a)^{2}+(12 + 2b)^{2}=4a^{2}+144+48b+4b^{2},$$GB^{2}=(3a)^{2}+(8 - 3b)^{2}=9a^{2}+64-48b+9b^{2},$
∴$ED^{2}+GB^{2}=13(a^{2}+b^{2})+208=13×4+208=260.$
∴$DE^{2}+BG^{2}$的值为260.

解析
(1)能.
证明如下:
∵四边形AEFG为正方形,
∴AE=AG,∠EAG=90°.
∵四边形ABCD为正方形,
∴AB=AD,∠BAD=90°,
∴∠EAB=∠GAD.
∴△AEB≌△AGD(SAS),
∴BE=DG.
(2)当∠EAG=∠BAD时,BE=DG.
理由如下:
∵∠EAG=∠BAD,
∴∠EAB=∠GAD.
∵四边形AEFG和四边形ABCD均为菱形,
∴AE=AG,AB=AD.
∴△AEB≌△AGD(SAS),
∴BE=DG.
(3)过E作EM⊥DA的延长线于点M,过G作GN⊥AB于点N.
∵$\frac{AE}{AG}=\frac{AB}{AD}=\frac{2}{3},$AE=4,AB=8,
∴AG=6,AD=12.
∵∠EAG=∠MAN=90°,
∴∠MAE=∠NAG.
又
∵∠AME=∠ANG,
∴△AME∽△ANG,
∴$\frac{ME}{NG}=\frac{AM}{AN}=\frac{AE}{AG}=\frac{2}{3}.$设EM=2a,AM=2b,
则GN=3a,AN=3b,$4a^{2}+4b^{2}=16,$
∴BN=8 - 3b,$a^{2}+b^{2}=4,$
∴$ED^{2}=(2a)^{2}+(12 + 2b)^{2}=4a^{2}+144+48b+4b^{2},$$GB^{2}=(3a)^{2}+(8 - 3b)^{2}=9a^{2}+64-48b+9b^{2},$
∴$ED^{2}+GB^{2}=13(a^{2}+b^{2})+208=13×4+208=260.$
∴$DE^{2}+BG^{2}$的值为260.

查看更多完整答案,请扫码查看


