《2025年5年中考3年模拟数学广东专版》

1.(2020广州,10,3分)如图,矩形ABCD的对角线AC,BD交于点O,AB = 6,BC = 8,过点O作OE⊥AC,交AD于点E,过点E作EF⊥BD,垂足为F,则OE + EF的值为　　　　　(　　　)

A.$\frac{48}{5}$　　
　B.$\frac{32}{5}$　　
　C.$\frac{24}{5}$　　
　D.$\frac{12}{5}$

答案： 5年中考
1.C
∵四边形ABCD为矩形，
∴∠ABC = 90°，AD//BC，OA = OD，
∴AC = $\sqrt{AB^{2}+BC^{2}}=\sqrt{6^{2}+8^{2}} = 10$，
∴$\sin\angle ACB=\frac{AB}{AC}=\frac{6}{10}=\frac{3}{5}$。
∵AD//BC，OA = OD，
∴∠ODA = ∠DAO = ∠ACB。
∴$\sin\angle ODA=\sin\angle DAO=\sin\angle ACB=\frac{3}{5}$。在Rt△AOE和Rt△DEF中，$OE = AE\cdot\sin\angle OAD=\frac{3}{5}AE$，
$EF = DE\cdot\sin\angle ODA=\frac{3}{5}DE$，
∴$OE + EF=\frac{3}{5}AE+\frac{3}{5}DE=\frac{3}{5}(AE + DE)=\frac{3}{5}AD=\frac{3}{5}\times8=\frac{24}{5}$。

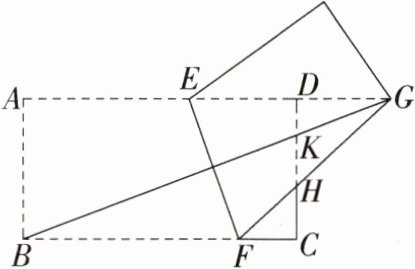
2.(2020深圳,12,3分)如图,矩形纸片ABCD中,AB = 6,BC = 12.将纸片折叠,使点B落在边AD的延长线上的点G处,折痕为EF,点E、F分别在边AD和边BC上.连接BG,交CD于点K,FG交CD于点H.给出以下结论:①EF⊥BG;②GE = GF;③△GDK和△GKH的面积相等;④当点F与点C重合时,∠DEF = 75°.其中正确的结论共有　　　　　　(　　　)

A.1个　
　B.2个　
　C.3个　
　D.4个

答案： 2.C　由折叠可知，点G是点B关于折痕EF的对称点。设EF交BG于点O，根据对称点的连线被对称轴垂直平分，可知EF⊥BG，BO = GO，故①正确。
∵四边形ABCD是矩形，
∴AD//BC，
∴∠EGO = ∠FBO。
又
∵BO = GO，∠EOG = ∠FOB = 90°，
∴△EGO≌△FBO，
∴GE = BF。
又由折叠可知BF = GF，
∴GE = GF，故②正确。
过点K作KM⊥HG于M，
∵∠DGB = ∠GBC，BF = FG，
∴∠DGB = ∠GBC = ∠HGK，即GB是∠AGF的平分线。
又
∵CD⊥AD，KM⊥HG，
∴DK = KM。
在Rt△DGH中，HG＞DG，
∴△HGK的面积大于△DGK的面积，故③错误。
当点F与点C重合时，在Rt△CDG中，CD = AB = 6，CG = BC = 12，
∴∠CGD = 30°。
由②知GE = BC，
∴四边形BCGE为平行四边形。
又
∵BC = GC，
∴四边形BCGE为菱形，
∴∠BEG = 180° - ∠CGD = 150°。
根据菱形的每条对角线平分一组对角，可知$\angle DEF=\frac{1}{2}\angle BEG=\frac{1}{2}\times150° = 75°$，故④正确。
正确的结论有①②④，共3个。

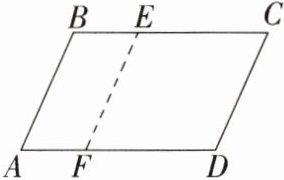
3.(2023深圳,5,3分)如图,在平行四边形ABCD中,AB = 4,BC = 6,将线段AB水平向右平移a个单位长度得到线段FE,当四边形ECDF为菱形时,a的值为　　　　　(　　　)

A.1　　　
　B.2　　
　C.3　　
　D.4

答案： 3.B
∵将线段AB水平向右平移a个单位长度得到线段FE，
∴AB = EF = 4，BE = a。
∵四边形ECDF是菱形，
∴EC = EF = 4，
∴BE = BC - EC = 6 - 4 = 2，
∴a = 2。

4.(2022广东,13,3分)菱形的边长为5,则它的周长为________.

答案： 答案　20

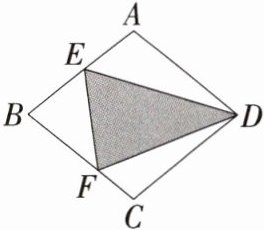
5.(2024广东,15,3分)如图,菱形ABCD的面积为24,点E是AB的中点,点F是BC上的动点.若△BEF的面积为4,则图中阴影部分的面积为________.

答案：
答案　10
解析　连接BD，
∵E是AB的中点，
∴$S_{\triangle AED}=\frac{1}{2}S_{\triangle ABD}=\frac{1}{4}S_{菱形ABCD}=\frac{1}{4}\times24 = 6$。
连接EC，

同理可得$S_{\triangle BEC}=S_{\triangle AED}=6$。
∵$S_{\triangle BEF}=4$，
∴$S_{\triangle BEF}=\frac{2}{3}S_{\triangle BEC}$，
∴$FC=\frac{1}{3}BC$，
∴$S_{\triangle DFC}=\frac{1}{3}S_{\triangle BCD}=\frac{1}{6}S_{菱形ABCD}=\frac{1}{6}\times24 = 4$。
∴$S_{阴影}=S_{菱形ABCD}-S_{\triangle AED}-S_{\triangle BEF}-S_{\triangle DFC}=24 - 6 - 4 - 4 = 10$。

6.(2024广东,7,3分)完全相同的4个正方形面积之和是100,则正方形的边长是　　(　　　)
A.2　　
　B.5　　
　C.10　　
　D.20

答案： 6.B

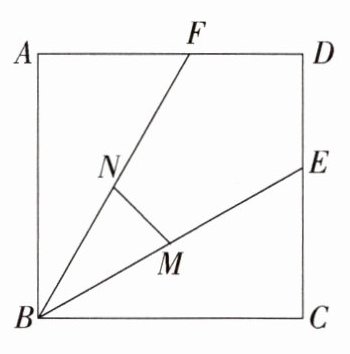
7.(2022广州,9,3分)如图,正方形ABCD的面积为3,点E在边CD上,且CE = 1,∠ABE的平分线交AD于点F,点M,N分别是BE,BF的中点,则MN的长为　　　　(　　　)


A.$\frac{\sqrt{6}}{2}$　　
　B.$\frac{\sqrt{3}}{2}$　　
　C.2 - $\sqrt{3}$　
　D.$\frac{\sqrt{6}-\sqrt{2}}{2}$

答案：
7.D　如图，连接EF，过点F作FG⊥BE于点G，

∵正方形的面积为3，
∴正方形的边长为$\sqrt{3}$。
∵CE = 1，
∴在Rt△BEC中，BE = $\sqrt{BC^{2}+EC^{2}} = 2$。
∵BF平分∠ABE，FA⊥AB，FG⊥BE，
∴FG = FA。
易证△FAB≌△FGB，
∴BG = BA=$\sqrt{3}$，
∴EG = BE - BG = 2-$\sqrt{3}$。
∵CD=$\sqrt{3}$，
∴DE=$\sqrt{3}-1$。
设AF = FG = x，则FD=$\sqrt{3}-x$。
在Rt△DFE和Rt△FGE中，$FD^{2}+DE^{2}=FG^{2}+GE^{2}=FE^{2}$，
∴$(\sqrt{3}-x)^{2}+(\sqrt{3}-1)^{2}=x^{2}+(2 - \sqrt{3})^{2}$，解得x = 1。
∴FG = AF = 1。
∴$FE=\sqrt{FG^{2}+GE^{2}}=\sqrt{1^{2}+(2 - \sqrt{3})^{2}}=\sqrt{8 - 4\sqrt{3}}=\sqrt{6}-\sqrt{2}$。
∵点M，N分别为BE，BF的中点，
∴MN为△BEF的中位线，
∴$MN=\frac{EF}{2}=\frac{\sqrt{6}-\sqrt{2}}{2}$。

8.(2020广东,9,3分)如图,在正方形ABCD中,AB = 3,点E,F分别在边AB,CD上,∠EFD = 60°.若将四边形EBCF沿EF折叠,点B恰好落在AD边上,则BE的长为 (　　　)


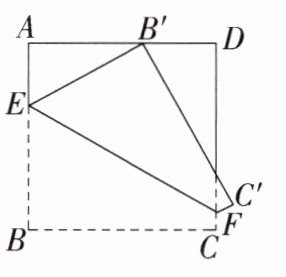
A.1　　　
　B.$\sqrt{2}$　　
　C.$\sqrt{3}$　　
　D.2

答案： 8.D
∵四边形ABCD是正方形，
∴CD//AB，
∴∠EFD = ∠FEB = 60°。
由折叠的性质可知∠FEB = ∠FEB' = 60°，
∴∠AEB' = 180° - ∠FEB - ∠FEB' = 60°，
∴∠AB'E = 30°，
∴B'E = 2AE。
设AE = x，则BE = B'E = 2x，
∴AB = AE + BE = 3x = 3，
∴x = 1，
∴BE = 2x = 2。

9.(2021广东,23,8分)如图,边长为1的正方形ABCD中,点E为AD的中点.连接BE,将△ABE沿BE折叠得到△FBE,BF交AC于点G,求CG的长.

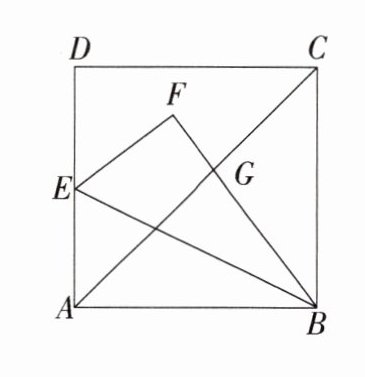
答案：
9.解析　延长BF交CD于点H，连接EH。

在正方形ABCD中，DC//AB，∠D = ∠DAB = ∠DCB = 90°，DC = DA = AB = BC = 1，AC=$\sqrt{2}$。
由题意可知FE = AE，AB = FB，∠EFB = ∠EAB = 90°，
∴∠EFH = 90°。
∵E是AD的中点，
∴AE = DE，
∴FE = DE。
又EH = EH，
∴Rt△DEH≌Rt△FEH，
∴DH = FH。
设DH = FH = x(x＞0)，则HC = 1 - x，BH = 1 + x。
在Rt△CHB中，$BC^{2}+CH^{2}=HB^{2}$，
即$1^{2}+(1 - x)^{2}=(1 + x)^{2}$，解得$x=\frac{1}{4}$。
∴$HC = DC - DH = 1-\frac{1}{4}=\frac{3}{4}$。
∵DC//AB，
∴△HGC∽△BGA。
∴$\frac{CG}{AG}=\frac{HC}{BA}=\frac{3}{4}$，
即$\frac{CG}{AC - CG}=\frac{3}{4}$，
∴$CG=\frac{3\sqrt{2}}{7}$。

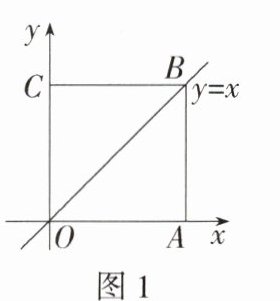
10.(2023广东,23,12分)综合运用
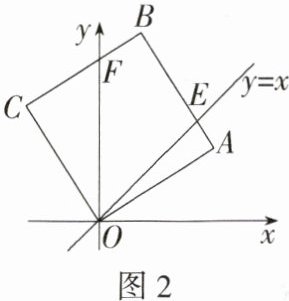
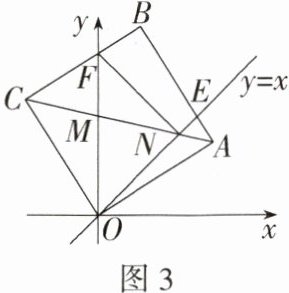
如图1,在平面直角坐标系中,正方形OABC的顶点A在x轴的正半轴上.如图2,将正方形OABC绕点O逆时针旋转,旋转角为α(0° ＜ α ＜ 45°),AB交直线y = x于点E,BC交y轴于点F.
(1)当旋转角∠COF为多少度时,OE = OF?(直接写出结果,不要求写解答过程)
(2)若点A(4,3),求FC的长.
(3)如图3,对角线AC交y轴于点M,交直线y = x于点N,连接FN.将△OFN与△OCF的面积分别记为S₁与S₂.设S = S₁ - S₂,AN = n,求S关于n的函数表达式.

答案：
10.解析　
(1)22.5°。
详解：当OE = OF时，
易证△OCF≌△OAE，
∴∠COF = ∠AOE = 22.5°。
(2)延长BA交x轴于点D，过点A作AG⊥x轴，垂足为G。

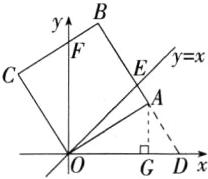
在正方形OABC中，OC = OA，∠C = ∠BAO = ∠OAD = 90°。
由旋转性质得∠COF = ∠AOD。
∴△OCF≌△OAD。
∴AD = CF。
∵∠OAG + ∠GAD = 90°，∠ADG + ∠GAD = 90°，
∴∠OAG = ∠ADG。
∵∠AGD = ∠AGO = 90°，
∴△GDA∽△GAO。
∴$\frac{AG}{OG}=\frac{GD}{AG}$。
∵A(4，3)，
∴OG = 4，AG = 3，
∴$GD=\frac{9}{4}$。
由勾股定理得$AD=\sqrt{AG^{2}+GD^{2}}=\sqrt{3^{2}+(\frac{9}{4})^{2}}=\frac{15}{4}$，
∴$FC=\frac{15}{4}$。
(3)延长BA交x轴于点D，连接ND，如图。

∵∠FCM = ∠NOM = 45°，∠CMF = ∠OMN，
∴△CMF∽△OMN。
∴$\frac{CM}{OM}=\frac{FM}{MN}$，
即$\frac{CM}{FM}=\frac{OM}{MN}$。
又∠CMO = ∠FMN，
∴△CMO∽△FMN，
∴∠OFN = ∠OCN = 45°。
又∠FON = 45°，
∴∠ONF = 90°。
易知△AOD≌△COF，①
∴OF = OD。
又∠FOE = ∠DOE = 45°，
∴△FON≌△DON。②
∴∠OND = ∠ONF = 90°。
又∠NOD = 45°，
∴NO = ND。
∵∠OAE = ∠OND = ∠DNE = 90°，
∴∠NOH = ∠NDE。
∴△ONH≌△DNE。③
∴NE = NH。
过N作NP⊥OA，垂足为P，过N作NQ⊥AB，垂足为Q。
∵∠OAC = ∠BAC = 45°，
∴NP = NQ。
∴Rt△NPH≌Rt△NQE。④
$S = S_{\triangle OFN}-S_{\triangle OCF}=S_{\triangle ODN}-S_{\triangle ODA}$（由①，②得）
$=S_{\triangle OHN}-S_{\triangle DHA}=S_{\triangle OAE}-S_{\triangle DNE}$
$=S_{四边形NHAE}$（由③得）
$=S_{正方形NPAQ}$（由④得）
$=\frac{1}{2}AN^{2}=\frac{1}{2}n^{2}$。
即$S=\frac{1}{2}n^{2}$。
一题多解
(3)过点N作直线PQ⊥BC于点P，交OA于点Q。

∵四边形OABC是正方形，
∴∠BCA = ∠OCA = 45°，BC//OA。
又∠FON = 45°，
∴∠FCN = ∠FON = 45°，
∴F、C、O、N四点共圆，
∴∠OFN = ∠OCA = 45°，
∴∠OFN = ∠FON = 45°，
∴△FON是等腰直角三角形，
∴FN = NO，∠FNO = 90°，
∴∠FNP + ∠ONQ = 90°。
又
∵∠NOQ + ∠ONQ = 90°，
∴∠NOQ = ∠FNP，
∴△NOQ≌△FNP(AAS)，
∴NP = OQ，FP = NQ。
易得四边形OQPC是矩形，
∴CP = OQ，OC = PQ。
∴$S_{1}=S_{\triangle OFN}=\frac{1}{2}ON^{2}$
$=\frac{1}{2}(OQ^{2}+NQ^{2})$
$=\frac{1}{2}PN^{2}+\frac{1}{2}NQ^{2}$。
$S_{2}=S_{\triangle OCF}=\frac{1}{2}CF\cdot OC$
$=\frac{1}{2}(PC - PF)\cdot(PN + NQ)$
$=\frac{1}{2}(PN - NQ)\cdot(PN + NQ)$
$=\frac{1}{2}PN^{2}-\frac{1}{2}NQ^{2}$。
∴$S = S_{1}-S_{2}=NQ^{2}$。
易得△ANQ为等腰直角三角形，
∴$NQ=\frac{\sqrt{2}}{2}AN=\frac{\sqrt{2}}{2}n$，
∴$S = NQ^{2}=(\frac{\sqrt{2}}{2}n)^{2}=\frac{1}{2}n^{2}$。
∴S关于n的函数表达式为$S=\frac{1}{2}n^{2}$。