《2025年5年中考3年模拟数学广东专版》

答案： 答案　①各边
@@答案　②$(n - 2)\times180^{\circ}$　③$360^{\circ}$　④$(n - 3)$　⑤$\frac{n(n - 3)}{2}$
@@答案　⑥$\frac{(n - 2)\times180^{\circ}}{n}$　⑦$\frac{360^{\circ}}{n}$　⑧$108^{\circ}$

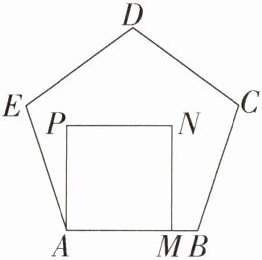
例1　如图,正方形AMNP的边AM在正五边形ABCDE的边AB上,则∠PAE = ________.
　　　　　　　
解题思路　利用多边形内角和公式,可求出∠EAB = $\frac{(5 - 2)\times180^{\circ}}{5}$ = 108°,又∠PAM = 90°,即可求出∠PAE.

答案： 答案　18°
解析
∵五边形ABCDE为正五边形,
∴∠EAB=$\frac{(5 - 2)\times180°}{5}$=108°,
∵四边形AMNP为正方形，
∴∠PAM=90°,
∴∠PAE=∠EAB−∠PAM=108°−90°=18°.

变式1　正多边形的一个外角等于60°,这个多边形的边数是 (　　)
A.3
B.6
C.9
D.12

答案： B　根据正多边形的外角和为360°求得此多边形的边数为360°÷60°=6.

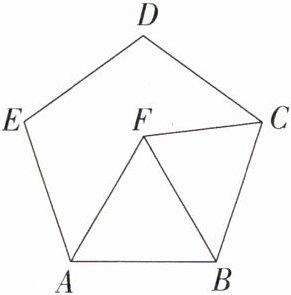
变式2　如图,点F在正五边形ABCDE的内部,△ABF为等边三角形,则∠AFC等于 (　　)
　　　　　　　

A.108°
B.120°
C.126°
D.132°

答案： C
∵△ABF为等边三角形,
∴AB=AF=BF,∠AFB=∠ABF =60°.
又
∵五边形ABCDE是正五边形，
∴　BC=AB　=BF,　∠ABC=$\frac{(5 - 2)\times180°}{5}$=108°.
∴　∠FBC=∠ABC−∠ABF=108°−60°=48°,
∴∠BFC=$\frac{180° - ∠FBC}{2}$=$\frac{180° - 48°}{2}$=66°,
∴∠AFC=∠AFB+∠BFC=60°+66°=126°.