《2025年5年中考3年模拟数学广东专版》

变式1　如图,在△ABC中,AB=AC,∠B=70°.以点C为圆心,CA长为半径作弧,交直线BC于点P,连接AP,则∠BAP的度数是________.

答案：
变式1 答案 15°或75°
解析 如图所示,
当点P在点B的左侧时,记为P₁,

∵AB = AC,∠ABC = 70°,
∴∠ACB = ∠ABC = 70°,
∴∠BAC = 180°-∠ACB-∠ABC = 40°,
∵CA = CP₁,
∴∠CAP₁ = ∠CP₁A=$\frac{180°-∠ACP₁}{2}$= 55°,
∴∠BAP₁ = ∠CAP₁-∠CAB = 55°-40° = 15°;
当点P在点C的右侧时,记为P₂,
∵CA = CP₂,
∴∠CAP₂ = ∠CP₂A=$\frac{70°}{2}$= 35°,
∴∠BAP₂ = ∠CAP₂+∠BAC = 35°+40° = 75°.综上,∠BAP的度数是15°或75°.

例2　《九章算术》中有一道“引葭赴岸”问题:“今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适与岸齐.问水深,葭长各几何？”题意是:有一个池塘,其底面是边长为10尺的正方形,一棵芦苇AB生长在它的中央,高出水面部分BC为1尺.如果把芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B 恰好碰到岸边的B'(示意图如图),则水深为______尺.
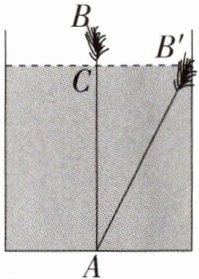
解题思路　设芦苇长x尺,则水深(x−1)尺,根据题意得Rt△ACB'各边长,进而根据勾股定理求解.

答案： 例2 答案 12
解析 设芦苇长AB = AB' = x尺,则水深AC = (x - 1)尺,根据“底面是边长为10尺的正方形,一棵芦苇AB生长在它的中央”可得B'C = 5尺,在Rt△AB'C中,5²+(x - 1)² = x²,解得x = 13,即芦苇长13尺,水深12尺.

例3　若直角三角形的边长分别为3cm,4cm,则斜边上的中线长为________.
解题关键点　　斜边、直角边并不明确,需分类讨论.

答案： 例3 答案 2.5 cm或2 cm
解析 分两种情况:
当4 cm为直角三角形的斜边长时,斜边上的中线长=$\frac{1}{2}$×4 = 2(cm);
当4 cm为直角三角形的直角边长时,根据勾股定理得,
斜边长=$\sqrt{3^{2}+4^{2}}$ = 5(cm),
∴斜边上的中线长=$\frac{1}{2}$×5 = 2.5(cm).
综上,斜边上的中线长为2.5 cm或2 cm.

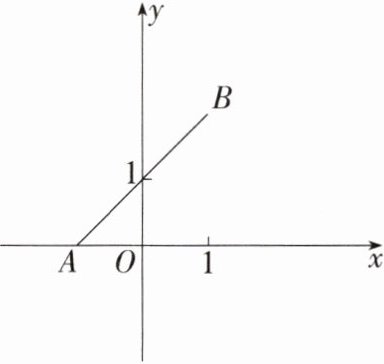
变式2　如图,已知点A(−1,0)和点B(1,2),在坐标轴上确定点P,使得△ABP为直角三角形，则满足条件的点P共有　　　　　　　　(　　　)

A.2个　　
　B.4个　
　C.6个　
　D.7个

答案： 变式2 C 易知AB = 2$\sqrt{2}$,△ABP为直角三角形,分两种情况:
当点P在x轴上时,设点P坐标为(m,0),则AP=$\sqrt{(m + 1)^{2}}$,
BP=$\sqrt{(m - 1)^{2}+4}$.
若∠APB = 90°,则AP²+BP² = AB²,
即(m + 1)²+(m - 1)²+4 = 8,
解得m = 1或m = - 1(舍去);
若∠PAB = 90°,则AP²+AB² = BP²,
即(m + 1)²+8 = (m - 1)²+4,
解得m = - 1(舍去);
若∠PBA = 90°,则BP²+AB² = AP²,即(m - 1)²+4+8 = (m + 1)²,解得m = 3.
当点P在y轴上时,设点P坐标为(0,n),
同理可得n = 1-$\sqrt{2}$,1+$\sqrt{2}$,- 1,3.
综上,满足题意的点P有(1,0)、(3,0)、(0,1-$\sqrt{2}$)、(0,1+$\sqrt{2}$)、(0,- 1)、(0,3),共6个.

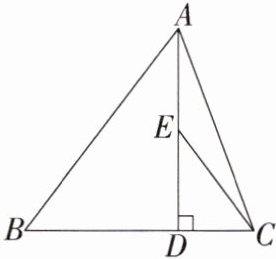
变式3　如图,在△ABC中,已知AB=2,AD⊥BC,垂足为D,BD=2CD.若E是AD的中点,则EC=________.

答案： 变式3 答案 1
解析 设AE = ED = x,CD = y,
∴BD = 2y,
∵AD⊥BC,
∴∠ADB = ∠ADC = 90°,
∴在Rt△ABD中,AB² = 4x²+4y²,
即x²+y² = 1,在Rt△CDE中,EC² = x²+y² = 1,
∴EC = 1.