第70页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
1.(2023广东,6,3分)我国著名数学家华罗庚曾为普及优选法作出重要贡献.优选法中有一种0.618法应用了 ( )
A.黄金分割数
B.平均数
C.众数
D.中位数
A.黄金分割数
B.平均数
C.众数
D.中位数
答案:
A 黄金分割比为$\frac{\sqrt{5}-1}{2}\approx0.618$.
2.(2018广东,7,3分)在△ABC中,点D、E分别为边AB、AC的中点,则△ADE与△ABC的面积之比为 ( )
A.$\frac{1}{2}$
B.$\frac{1}{3}$
C.$\frac{1}{4}$
D.$\frac{1}{6}$
A.$\frac{1}{2}$
B.$\frac{1}{3}$
C.$\frac{1}{4}$
D.$\frac{1}{6}$
答案:
因为D、E分别是边AB、AC的中点,所以DE是△ABC的中位线,所以DE//BC,所以△ADE∽△ABC,且相似比是$\frac{1}{2}$,所以它们的面积比为$\frac{1}{4}$.
3.(2023广东,15,3分)边长分别为10,6,4的三个正方形拼接在一起,它们的底边在同一直线上(如图),则图中阴影部分的面积为________.


答案:
答案 15
解析 如图,

∵BF//DE,
∴△ABF∽△ADE,
∴$\frac{AB}{AD}=\frac{BF}{DE}$,
∵AB = 4,AD = 4 + 6 + 10 = 20,DE = 10,
∴$\frac{4}{20}=\frac{BF}{10}$,
∴BF = 2,
∴GF = 6 - 2 = 4.
∵CK//DE,
∴△ACK∽△ADE,
∴$\frac{AC}{AD}=\frac{CK}{DE}$,
∵AC = 4 + 6 = 10,AD = 20,DE = 10,
∴$\frac{10}{20}=\frac{CK}{10}$,
∴CK = 5,
∴HK = 6 - 5 = 1.
∴$S_{阴影}=\frac{1}{2}(HK + GF)\cdot GH$
=$\frac{1}{2}\times(1 + 4)\times6$
= 15.
答案 15
解析 如图,

∵BF//DE,
∴△ABF∽△ADE,
∴$\frac{AB}{AD}=\frac{BF}{DE}$,
∵AB = 4,AD = 4 + 6 + 10 = 20,DE = 10,
∴$\frac{4}{20}=\frac{BF}{10}$,
∴BF = 2,
∴GF = 6 - 2 = 4.
∵CK//DE,
∴△ACK∽△ADE,
∴$\frac{AC}{AD}=\frac{CK}{DE}$,
∵AC = 4 + 6 = 10,AD = 20,DE = 10,
∴$\frac{10}{20}=\frac{CK}{10}$,
∴CK = 5,
∴HK = 6 - 5 = 1.
∴$S_{阴影}=\frac{1}{2}(HK + GF)\cdot GH$
=$\frac{1}{2}\times(1 + 4)\times6$
= 15.
4.(2022深圳,15,3分)已知△ABC是直角三角形,∠ABC = 90°,AB = 3,BC = 5,AE = 2$\sqrt{5}$,连接CE,以CE为斜边作直角三角形CDE且CD = DE,F是AE边上的一点,连接BD和BF,且∠FBD = 45°,则AF长为________.
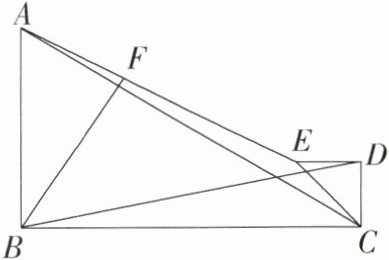

答案:
答案 $\frac{3\sqrt{5}}{4}$
解析 将线段BD绕点D顺时针旋转90°,得到线段HD,连接FH,EH,延长HE交BC于G,
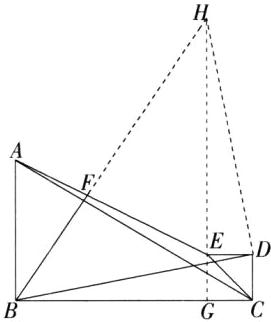
∴∠BDH = 90°,HD = BD,
又
∵△EDC是直角三角形,
∴∠EDH = ∠CDB,又ED = CD,
∴△EDH≌△CDB(SAS),
∴EH = CB = 5,∠EHD = ∠CBD,
∴∠BGH = ∠BDH = 90°,
∵△BDH是等腰直角三角形,
∴∠HBD = 45°,又∠FBD = 45°,
∴B、F、H三点共线.
∵∠BGH = 90°,∠ABC = 90°,
∴HE//AB,
∴△ABF∽△EHF,
∴$\frac{AB}{EH}=\frac{AF}{EF}=\frac{AF}{AE - AF}$,
∴$\frac{3}{5}=\frac{AF}{2\sqrt{5}-AF}$,
∴$AF=\frac{3\sqrt{5}}{4}$.
答案 $\frac{3\sqrt{5}}{4}$
解析 将线段BD绕点D顺时针旋转90°,得到线段HD,连接FH,EH,延长HE交BC于G,

∴∠BDH = 90°,HD = BD,
又
∵△EDC是直角三角形,
∴∠EDH = ∠CDB,又ED = CD,
∴△EDH≌△CDB(SAS),
∴EH = CB = 5,∠EHD = ∠CBD,
∴∠BGH = ∠BDH = 90°,
∵△BDH是等腰直角三角形,
∴∠HBD = 45°,又∠FBD = 45°,
∴B、F、H三点共线.
∵∠BGH = 90°,∠ABC = 90°,
∴HE//AB,
∴△ABF∽△EHF,
∴$\frac{AB}{EH}=\frac{AF}{EF}=\frac{AF}{AE - AF}$,
∴$\frac{3}{5}=\frac{AF}{2\sqrt{5}-AF}$,
∴$AF=\frac{3\sqrt{5}}{4}$.
5.(2018广州,16,3分)如图,CE是▱ABCD的边AB的垂直平分线,垂足为点O,CE与DA的延长线交于点E.连接AC,BE,DO,DO与AC交于点F.则下列结论:
①四边形ACBE是菱形$;②∠ACD = ∠BAE;③AF:BE = 2:3;④S_{四边形AFOE}:S_{△COD}= 2:3.$
其中正确的结论有________.(填写所有正确结论的序号)

①四边形ACBE是菱形$;②∠ACD = ∠BAE;③AF:BE = 2:3;④S_{四边形AFOE}:S_{△COD}= 2:3.$
其中正确的结论有________.(填写所有正确结论的序号)

答案:
答案 ①②④
解析 由CE是边AB的垂直平分线可得AC = CB,所以∠CAB = ∠CBA,由四边形ABCD是平行四边形可得AB//CD,AD//BC,所以∠CAB = ∠ACD,∠BAE = ∠CBA,所以∠CAB = ∠ACD = ∠BAE,故②正确.由∠CAO = ∠EAO,AO = AO,∠AOC = ∠AOE可得△AOC≌△AOE(ASA),从而AE = AC,又AC = BC,所以AE = BC,因为AE//CB,所以四边形ACBE是平行四边形,因为AC = BC,所以四边形ACBE是菱形,故①正确.由AO//CD,可得$\frac{AF}{FC}=\frac{AO}{DC}=\frac{EO}{EC}=\frac{1}{2}$,所以$\frac{AF}{BE}=\frac{AF}{AC}=\frac{1}{3}$,故③错误.设$S_{\triangle AFO}=S$,由$\frac{AF}{FC}=\frac{1}{2}$,可得$S_{\triangle CFO}=2S$,再根据△AFO∽△CFD可得$S_{\triangle DFC}=4S$,所以$S_{\triangle COD}=6S$,$S_{\triangle COA}=3S = S_{\triangle AOE}$,所以$S_{四边形AFOE}=4S$,所以$S_{四边形AFOE}:S_{\triangle COD}=4S:6S = 2:3$,故④正确.
解析 由CE是边AB的垂直平分线可得AC = CB,所以∠CAB = ∠CBA,由四边形ABCD是平行四边形可得AB//CD,AD//BC,所以∠CAB = ∠ACD,∠BAE = ∠CBA,所以∠CAB = ∠ACD = ∠BAE,故②正确.由∠CAO = ∠EAO,AO = AO,∠AOC = ∠AOE可得△AOC≌△AOE(ASA),从而AE = AC,又AC = BC,所以AE = BC,因为AE//CB,所以四边形ACBE是平行四边形,因为AC = BC,所以四边形ACBE是菱形,故①正确.由AO//CD,可得$\frac{AF}{FC}=\frac{AO}{DC}=\frac{EO}{EC}=\frac{1}{2}$,所以$\frac{AF}{BE}=\frac{AF}{AC}=\frac{1}{3}$,故③错误.设$S_{\triangle AFO}=S$,由$\frac{AF}{FC}=\frac{1}{2}$,可得$S_{\triangle CFO}=2S$,再根据△AFO∽△CFD可得$S_{\triangle DFC}=4S$,所以$S_{\triangle COD}=6S$,$S_{\triangle COA}=3S = S_{\triangle AOE}$,所以$S_{四边形AFOE}=4S$,所以$S_{四边形AFOE}:S_{\triangle COD}=4S:6S = 2:3$,故④正确.
6.(2024广州,18,4分)如图,点E,F分别在正方形ABCD的边BC,CD上,BE = 3,EC = 6,CF = 2.
求证:△ABE∽△ECF.
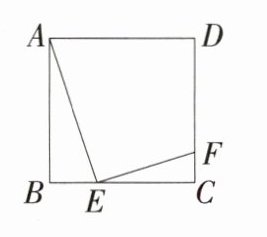
求证:△ABE∽△ECF.

答案:
证明
∵BE = 3,EC = 6,
∴BC = 9.
∵四边形ABCD是正方形,
∴AB = CB = 9,∠B = ∠C = 90°,
∵$\frac{AB}{EC}=\frac{9}{6}=\frac{3}{2}$,$\frac{BE}{CF}=\frac{3}{2}$,
∴$\frac{AB}{EC}=\frac{BE}{CF}$.
∴△ABE∽△ECF.
∵BE = 3,EC = 6,
∴BC = 9.
∵四边形ABCD是正方形,
∴AB = CB = 9,∠B = ∠C = 90°,
∵$\frac{AB}{EC}=\frac{9}{6}=\frac{3}{2}$,$\frac{BE}{CF}=\frac{3}{2}$,
∴$\frac{AB}{EC}=\frac{BE}{CF}$.
∴△ABE∽△ECF.
查看更多完整答案,请扫码查看


