《2025年5年中考3年模拟数学广东专版》

1.(2022广州,4,3分)点(3,−5)在正比例函数y = kx(k≠0)的图象上,则k的值为　　　(　　　)
A.−15　
　B.15　　
　C.−$\frac{3}{5}$　
　D.−$\frac{5}{3}$

答案： 5年中考
1.D 将(3,-5)代入y = kx中,得-5 = 3k,解得k = - $\frac{5}{3}$.

2.(2020广州,6,3分)一次函数y = -3x + 1的图象过点(x₁,y₁),(x₁ + 1,y₂),(x₁ + 2,y₃),则　　　　　　　　　　　　　　　(　　　)
A.y₁＜y₂＜y₃　　　　
　B.y₃＜y₂＜y₁
C.y₂＜y₁＜y₃　　　　
　D.y₃＜y₁＜y₂

答案： 2.B 对于一次函数y = -3x + 1,
∵ -3 ＜ 0,
∴ y随x的增大而减小,又x₁ ＜ x₁ + 1 ＜ x₁ + 2,
∴ y₃ ＜ y₂ ＜ y₁.

3.(2024广东,10,3分)已知不等式kx + b＜0的解集是x＜2,则一次函数y = kx + b的图象大致是　　　　　　　　　　　　　　　　(　　　)
　
　

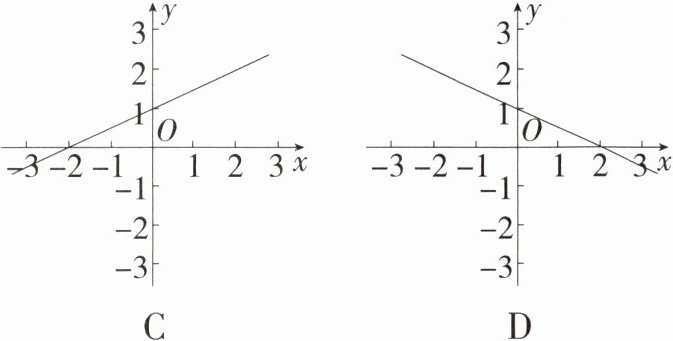
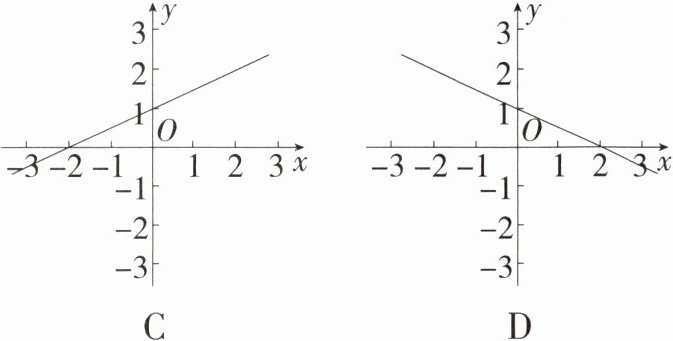
答案： 3.B A.由图象可得,不等式kx + b ＜ 0的解集是x ＞ -2,故本项不符合题意;
B.由图象可得,不等式kx + b ＜ 0的解集是x ＜ 2,故本项符合题意;
C.由图象可得,不等式kx + b ＜ 0的解集是x ＜ -2,故本项不符合题意;
D.由图象可得,不等式kx + b ＜ 0的解集是x ＞ 2,故本项不符合题意.

4.(2023广东,16(2),5分)已知一次函数y = kx + b的图象经过点(0,1)与点(2,5),求该一次函数的表达式.

答案： 4.解析 将(0,1)与(2,5)分别代入y = kx + b中,
得$\begin{cases}b = 1,\\2k + b = 5.\end{cases}$
解得$\begin{cases}k = 2,\\b = 1.\end{cases}$所以此一次函数的表达式为y = 2x + 1.

5.(2022广东,20,9分)物理实验证实:在弹性限度内,某弹簧长度y(cm)与所挂物体质量x(kg)满足函数关系y = kx + 15.下表是测量物体质量时,该弹簧长度与所挂物体质量的数量关系.
　　
　　　(1)求y与x的函数关系式;
　　　(2)当弹簧长度为20cm时,求所挂物体的质量.

答案： 5年中考
5.解析
(1)把x = 2,y = 19代入y = kx + 15中,得19 = 2k + 15,
解得k = 2,所以y与x的函数关系式为y = 2x + 15.
(2)把y = 20代入y = 2x + 15中,
得20 = 2x + 15,解得x = 2.5.
所以所挂物体的质量为2.5 kg.

6.(2023广州,22,10分)因活动需要购买某种水果,数学活动小组的同学通过市场调查得知:在甲商店购买该水果的费用y₁(元)与该水果的质量x(千克)之间的关系如图所示;在乙商店购买该水果的费用y₂(元)与该水果的质量x(千克)之间的函数解析式为y₂ = 10x(x≥0).
　　　(1)求y₁与x之间的函数解析式;
　　　(2)现计划用600元购买该水果,选甲、乙哪家商店能购买该水果更多一些？
　　　　　　　　　　　　　　

答案： 5年中考
6.解析
(1)当0≤x≤5时,设y₁ = kx(k≠0),
将(5,75)代入y₁ = kx,
得75 = 5k,解得k = 15,
∴ y₁ = 15x;
当x≥5时,设y₁ = mx + n(m≠0),
将(5,75),(10,120)代入y₁ = mx + n,
得$\begin{cases}5m + n = 75,\\10m + n = 120,\end{cases}$解得$\begin{cases}m = 9,\\n = 30,\end{cases}$
∴ y₁ =$\begin{cases}15x(0≤x≤5),\\9x + 30(x ＞ 5).\end{cases}$
(2)当y₁ = 600时,9x + 30 = 600,解得x = $\frac{190}{3}$;当y₂ = 600时,10x = 600,解得x = 60.
∵ $\frac{190}{3}$ ＞ 60,
∴ 选甲商店能购买该水果更多一些.