第109页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
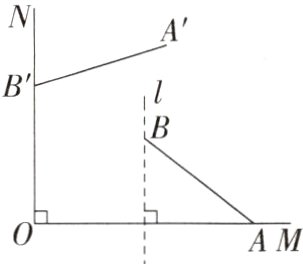
变式3 如图,射线OM、ON互相垂直,OA = 8,点B位于射线OM的上方,且在线段OA的垂直平分线l上,连接AB,AB = 5. 将线段AB绕点O按逆时针方向旋转得到对应线段A'B',若点B'恰好落在射线ON上,则点A'到射线ON的距离d = ______.

答案:
答案 $\frac{24}{5}$
解析 连接OA',OB,过A'作A'H⊥ON于点H,则A'H = d.

∵线段AB绕点O旋转得到A'B',
∴OA = OA',OB = OB',A'B' = AB = 5.
∵B在线段OA的垂直平分线上,
∴OB' = OB = BA = 5,
设B'H = x,
在Rt△A'HB'中,$x^{2}+d^{2}=5^{2}$,①
在Rt△A'HO中,$(x + 5)^{2}+d^{2}=8^{2}$,②
由①②解得$x=\frac{7}{5}$,
∴$d=\frac{24}{5}$(负舍).
答案 $\frac{24}{5}$
解析 连接OA',OB,过A'作A'H⊥ON于点H,则A'H = d.

∵线段AB绕点O旋转得到A'B',
∴OA = OA',OB = OB',A'B' = AB = 5.
∵B在线段OA的垂直平分线上,
∴OB' = OB = BA = 5,
设B'H = x,
在Rt△A'HB'中,$x^{2}+d^{2}=5^{2}$,①
在Rt△A'HO中,$(x + 5)^{2}+d^{2}=8^{2}$,②
由①②解得$x=\frac{7}{5}$,
∴$d=\frac{24}{5}$(负舍).
变式4 综合与实践
问题提出
某兴趣小组在一次综合与实践活动中提出这样一个问题:将足够大的直角三角板PEF(∠P = 90°,∠F = 60°)的一个顶点放在正方形中心O处,并绕点O逆时针旋转,探究直角三角板PEF与正方形ABCD重叠部分的面积变化情况(已知正方形边长为2).
操作发现
(1)如图1,若将三角板的顶点P放在点O处,在旋转过程中,当OF与OB重合时,重叠部分的面积为______;当OF与BC垂直时,重叠部分的面积为______;一般地,若正方形面积为S,在旋转过程中,重叠部分的面积S₁与S的关系为______.
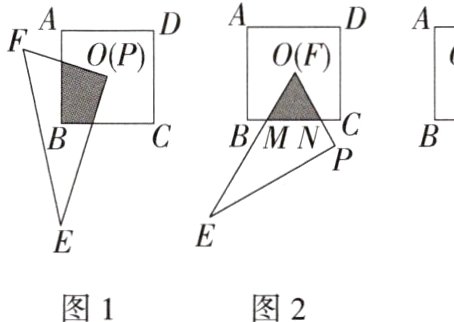
类比探究
(2)若将三角板的顶点F放在点O处,在旋转过程中,OE,OP分别与正方形的边相交于点M,N.
①如图2,当BM = CN时,试判断重叠部分△OMN的形状,并说明理由;
②如图3,当CM = CN时,求重叠部分四边形OMCN的面积(结果保留根号).
拓展应用
(3)若将任意一个锐角的顶点放在正方形中心O处,该锐角记为∠GOH(设∠GOH = α),将∠GOH绕点O逆时针旋转,在旋转过程中,∠GOH的两边与正方形ABCD的边所围成的图形的面积为S₂,请直接写出S₂的最小值与最大值(分别用含α的式子表示).
参考数据:sin 15°=(√6 - √2)/4,cos 15°=(√6 + √2)/4,tan 15°=2 - √3
请完成《精练册》对应练习P73 - P75
问题提出
某兴趣小组在一次综合与实践活动中提出这样一个问题:将足够大的直角三角板PEF(∠P = 90°,∠F = 60°)的一个顶点放在正方形中心O处,并绕点O逆时针旋转,探究直角三角板PEF与正方形ABCD重叠部分的面积变化情况(已知正方形边长为2).
操作发现
(1)如图1,若将三角板的顶点P放在点O处,在旋转过程中,当OF与OB重合时,重叠部分的面积为______;当OF与BC垂直时,重叠部分的面积为______;一般地,若正方形面积为S,在旋转过程中,重叠部分的面积S₁与S的关系为______.

类比探究
(2)若将三角板的顶点F放在点O处,在旋转过程中,OE,OP分别与正方形的边相交于点M,N.
①如图2,当BM = CN时,试判断重叠部分△OMN的形状,并说明理由;
②如图3,当CM = CN时,求重叠部分四边形OMCN的面积(结果保留根号).
拓展应用
(3)若将任意一个锐角的顶点放在正方形中心O处,该锐角记为∠GOH(设∠GOH = α),将∠GOH绕点O逆时针旋转,在旋转过程中,∠GOH的两边与正方形ABCD的边所围成的图形的面积为S₂,请直接写出S₂的最小值与最大值(分别用含α的式子表示).
参考数据:sin 15°=(√6 - √2)/4,cos 15°=(√6 + √2)/4,tan 15°=2 - √3
请完成《精练册》对应练习P73 - P75
答案:
解析
(1)1;1;$S_{1}=\frac{1}{4}S$.
详解:当OF与OB重合时,OE与OC重合,此时重叠部分为△OBC,重叠部分的面积为正方形ABCD面积的$\frac{1}{4}$,故$S_{重叠}=\frac{1}{4}\times2^{2}=1$.
当OF与BC垂直时,OE与CD垂直,重叠部分的面积为正方形ABCD面积的$\frac{1}{4}$,故$S_{重叠}=1$.
一般情况如图,连接OB,OC,
∵∠BOK + ∠BOR = 90°,∠COR + ∠BOR = 90°,
∴∠BOK = ∠COR,
∵∠OBK = ∠OCR = 45°,OB = OC,
∴△OBK≌△OCR(ASA),
∴$S_{重叠}=S_{\triangle OBC}=\frac{1}{4}S_{正方形ABCD}$,即$S_{1}=\frac{1}{4}S$.
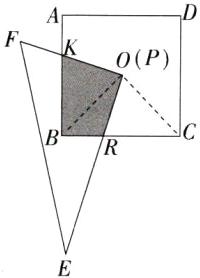
(2)①当BM = CN时,△OMN是等边三角形.理由如下:连接OB,OC,

∵四边形ABCD是正方形,且点O是正方形的中心,
∴OB = OC,∠OBC = ∠OCB = 45°,
∵BM = CN,
∴△OBM≌△OCN,
∴OM = ON,又
∵∠MON = 60°,
∴△OMN是等边三角形.
②连接OC,过点O作OJ⊥BC,垂足为J,易证△COM≌△CON,
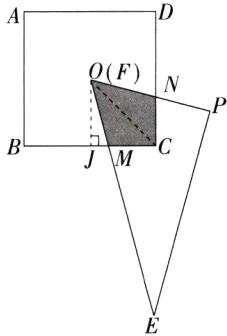
∴$∠COM=∠CON=\frac{1}{2}\times60^{\circ}=30^{\circ}$.
在等腰直角△OJC中,OJ = CJ = 1,$OC=\sqrt{2}$.
∵∠MOJ = 45° - 30° = 15°,
∴在Rt△OJM中,$JM=OJ\tan15^{\circ}=2-\sqrt{3}$,
∴$CM=1-(2 - \sqrt{3})=\sqrt{3}-1$,
∴$S_{\triangle CMO}=\frac{1}{2}CM\cdot OJ=\frac{1}{2}\times(\sqrt{3}-1)\times1=\frac{\sqrt{3}-1}{2}$,
∴四边形OMCN的面积=$2S_{\triangle CMO}=2\times\frac{\sqrt{3}-1}{2}=\sqrt{3}-1$.
(3)$S_{2}$的最小值为$\tan\frac{\alpha}{2}$,$S_{2}$的最大值为$1-\tan(45^{\circ}-\frac{\alpha}{2})$.
详解:过点O作OQ⊥BC,垂足为Q,则OQ = 1.
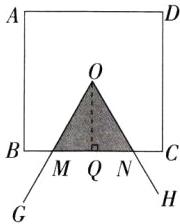
当BM = CN时,$S_{2}$取得最小值.
在Rt△OMQ中,$MQ=OQ\tan\frac{\alpha}{2}=\tan\frac{\alpha}{2}$,
∴$MN=2MQ=2\tan\frac{\alpha}{2}$,
∴$S_{2}=S_{\triangle OMN}=\frac{1}{2}MN\cdot OQ=\frac{1}{2}\times2\tan\frac{\alpha}{2}\times1=\tan\frac{\alpha}{2}$,即$S_{2}$的最小值为$\tan\frac{\alpha}{2}$.
过点O作OI⊥BC,垂足为I,连接OC,则OI = 1.当CM = CN时,$S_{2}$取得最大值,
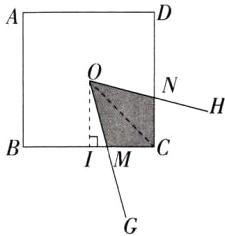
由
(2)②可知,此时$∠MOI=45^{\circ}-\frac{1}{2}\alpha$,
∴$MI=OI\cdot\tan∠MOI=\tan(45^{\circ}-\frac{1}{2}\alpha)$,
∴$MC=CI - MI=1-\tan(45^{\circ}-\frac{1}{2}\alpha)$,
∴$S_{\triangle MCO}=\frac{1}{2}MC\cdot OI=\frac{1}{2}\cdot[1-\tan(45^{\circ}-\frac{1}{2}\alpha)]\cdot1=\frac{1}{2}[1-\tan(45^{\circ}-\frac{1}{2}\alpha)]$,
∴$S_{2}$的最大值为$2S_{\triangle MCO}=1-\tan(45^{\circ}-\frac{1}{2}\alpha)$.
解析
(1)1;1;$S_{1}=\frac{1}{4}S$.
详解:当OF与OB重合时,OE与OC重合,此时重叠部分为△OBC,重叠部分的面积为正方形ABCD面积的$\frac{1}{4}$,故$S_{重叠}=\frac{1}{4}\times2^{2}=1$.
当OF与BC垂直时,OE与CD垂直,重叠部分的面积为正方形ABCD面积的$\frac{1}{4}$,故$S_{重叠}=1$.
一般情况如图,连接OB,OC,
∵∠BOK + ∠BOR = 90°,∠COR + ∠BOR = 90°,
∴∠BOK = ∠COR,
∵∠OBK = ∠OCR = 45°,OB = OC,
∴△OBK≌△OCR(ASA),
∴$S_{重叠}=S_{\triangle OBC}=\frac{1}{4}S_{正方形ABCD}$,即$S_{1}=\frac{1}{4}S$.

(2)①当BM = CN时,△OMN是等边三角形.理由如下:连接OB,OC,

∵四边形ABCD是正方形,且点O是正方形的中心,
∴OB = OC,∠OBC = ∠OCB = 45°,
∵BM = CN,
∴△OBM≌△OCN,
∴OM = ON,又
∵∠MON = 60°,
∴△OMN是等边三角形.
②连接OC,过点O作OJ⊥BC,垂足为J,易证△COM≌△CON,

∴$∠COM=∠CON=\frac{1}{2}\times60^{\circ}=30^{\circ}$.
在等腰直角△OJC中,OJ = CJ = 1,$OC=\sqrt{2}$.
∵∠MOJ = 45° - 30° = 15°,
∴在Rt△OJM中,$JM=OJ\tan15^{\circ}=2-\sqrt{3}$,
∴$CM=1-(2 - \sqrt{3})=\sqrt{3}-1$,
∴$S_{\triangle CMO}=\frac{1}{2}CM\cdot OJ=\frac{1}{2}\times(\sqrt{3}-1)\times1=\frac{\sqrt{3}-1}{2}$,
∴四边形OMCN的面积=$2S_{\triangle CMO}=2\times\frac{\sqrt{3}-1}{2}=\sqrt{3}-1$.
(3)$S_{2}$的最小值为$\tan\frac{\alpha}{2}$,$S_{2}$的最大值为$1-\tan(45^{\circ}-\frac{\alpha}{2})$.
详解:过点O作OQ⊥BC,垂足为Q,则OQ = 1.

当BM = CN时,$S_{2}$取得最小值.
在Rt△OMQ中,$MQ=OQ\tan\frac{\alpha}{2}=\tan\frac{\alpha}{2}$,
∴$MN=2MQ=2\tan\frac{\alpha}{2}$,
∴$S_{2}=S_{\triangle OMN}=\frac{1}{2}MN\cdot OQ=\frac{1}{2}\times2\tan\frac{\alpha}{2}\times1=\tan\frac{\alpha}{2}$,即$S_{2}$的最小值为$\tan\frac{\alpha}{2}$.
过点O作OI⊥BC,垂足为I,连接OC,则OI = 1.当CM = CN时,$S_{2}$取得最大值,

由
(2)②可知,此时$∠MOI=45^{\circ}-\frac{1}{2}\alpha$,
∴$MI=OI\cdot\tan∠MOI=\tan(45^{\circ}-\frac{1}{2}\alpha)$,
∴$MC=CI - MI=1-\tan(45^{\circ}-\frac{1}{2}\alpha)$,
∴$S_{\triangle MCO}=\frac{1}{2}MC\cdot OI=\frac{1}{2}\cdot[1-\tan(45^{\circ}-\frac{1}{2}\alpha)]\cdot1=\frac{1}{2}[1-\tan(45^{\circ}-\frac{1}{2}\alpha)]$,
∴$S_{2}$的最大值为$2S_{\triangle MCO}=1-\tan(45^{\circ}-\frac{1}{2}\alpha)$.
查看更多完整答案,请扫码查看


