第1页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
1. 下列方程中,一定是关于x的一元二次方程的是 (
A. $x^{2}-2x-3= 0$
B. $2x^{2}-y-1= 0$
C. $x^{2}-x(x+7)= 0$
D. $ax^{2}+bx+c= 0$
A
)A. $x^{2}-2x-3= 0$
B. $2x^{2}-y-1= 0$
C. $x^{2}-x(x+7)= 0$
D. $ax^{2}+bx+c= 0$
答案:
A
2. 将方程$7x-3= 2x^{2}$化为一般形式后,常数项为3,则一次项系数为 (
A. 7
B. -7
C. 7x
D. -7x
B
)A. 7
B. -7
C. 7x
D. -7x
答案:
B
3. 已知方程$3x^{2}-(k-1)x+3k+2= 0$有一个根是-1,则k的值是 (
A. -3
B. -1
C. 1
D. 2
B
)A. -3
B. -1
C. 1
D. 2
答案:
B
4. 已知$(m-1)x^{|m+1|}+3x-5= 0$是一元二次方程,则$m=$
$-3$
.
答案:
$-3$
5. 若关于x的一元二次方程$x^{2}-ax-2a+1= 0$的二次项系数、一次项系数及常数项之和为-4,则a的值为
2
.
答案:
2
6. 根据下列问题,列出关于x的方程,并将其化为一元二次方程的一般形式:
(1) 两个连续偶数的积是120,求这两个数中较小的数;
(2) 绿苑小区住宅设计中,准备在每两幢楼房之间,开辟一块面积为$900m^{2}$的矩形绿地,并且长比宽多11m,那么绿地的长为多少?
(3) 某种产品原来成本价是25元,后经过技术改进,连续二次降低成本,现在这种产品的成本价仅16元,试问平均每次降低成本的百分率为多少?
(1) 两个连续偶数的积是120,求这两个数中较小的数;
(2) 绿苑小区住宅设计中,准备在每两幢楼房之间,开辟一块面积为$900m^{2}$的矩形绿地,并且长比宽多11m,那么绿地的长为多少?
(3) 某种产品原来成本价是25元,后经过技术改进,连续二次降低成本,现在这种产品的成本价仅16元,试问平均每次降低成本的百分率为多少?
答案:
解:
(1)设较小的偶数为$x$,则较大的偶数为$x + 2$,依题意得$x(x + 2) = 120$,即$x^{2} + 2x - 120 = 0$;
(2)设宽为$x\mathrm{m}$,长为$(x + 11)\mathrm{m}$,依题意得$x(x + 11) = 900$,即$x^{2} + 11x - 900 = 0$;
(3)设平均每次降低成本的百分率为$x$,依题意得$25(1 - x)^{2} = 16$,即$25x^{2} - 50x + 9 = 0$。
(1)设较小的偶数为$x$,则较大的偶数为$x + 2$,依题意得$x(x + 2) = 120$,即$x^{2} + 2x - 120 = 0$;
(2)设宽为$x\mathrm{m}$,长为$(x + 11)\mathrm{m}$,依题意得$x(x + 11) = 900$,即$x^{2} + 11x - 900 = 0$;
(3)设平均每次降低成本的百分率为$x$,依题意得$25(1 - x)^{2} = 16$,即$25x^{2} - 50x + 9 = 0$。
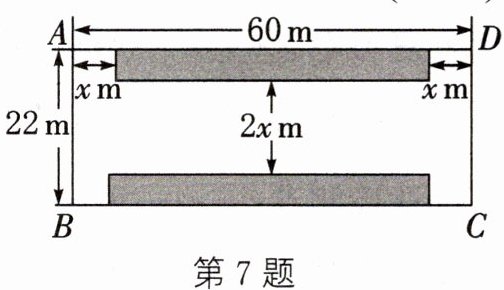
7. (2024·西宁)如图,小区物业规划在一个长60m,宽22m的矩形场地ABCD上,修建一个小型停车场,阴影部分为停车位所在区域,两侧是宽xm的道路,中间是宽2xm的道路.如果阴影部分的总面积是$600m^{2}$,那么x满足的方程是 (
A. $x^{2}-41x+180= 0$
B. $x^{2}-41x+225= 0$
C. $x^{2}-41x+30= 0$
D. $x^{2}-41x-270= 0$
A
)
A. $x^{2}-41x+180= 0$
B. $x^{2}-41x+225= 0$
C. $x^{2}-41x+30= 0$
D. $x^{2}-41x-270= 0$
答案:
A
8. (2024·凉山州)若关于x的一元二次方程$(a+2)x^{2}+x+a^{2}-4= 0$的一个根是x= 0,则a的值为 (
A. 2
B. -2
C. 2或-2
D. $\frac{1}{2}$
A
)A. 2
B. -2
C. 2或-2
D. $\frac{1}{2}$
答案:
A
9. 若方程$(m^{2}-1)x^{2}+\sqrt{m+1}x-1= 0$是关于x的一元二次方程,则m的取值范围是
$m > -1$且$m \neq 1$
.
答案:
$m > -1$且$m \neq 1$
查看更多完整答案,请扫码查看


