2025年金版新学案高中数学选择性必修第一册北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年金版新学案高中数学选择性必修第一册北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第63页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
典例 3 (1)已知 $ F $ 是双曲线 $\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}} = 1(a > 0,b > 0)$ 的焦点,$ B $ 是虚轴的一个端点,线段 $ BF $ 与双曲线交于点 $ M $,且点 $ M $ 恰是线段 $ BF $ 的中点,则双曲线的离心率为(
A.$\frac{\sqrt{5}}{2}$
B.$\sqrt{3}$
C.$ 2 $
D.$\sqrt{5}$
D
)A.$\frac{\sqrt{5}}{2}$
B.$\sqrt{3}$
C.$ 2 $
D.$\sqrt{5}$
答案:
典例3
(1)D
(1)不妨设$F(-c,0),B(0,b)$,则$M(-\frac{c}{2},\frac{b}{2})$.将点$M$坐标代入双曲线方程$\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1$,得$\frac{c^{2}}{4a^{2}}-\frac{1}{4}=1$,则$\frac{c^{2}}{4a^{2}}=\frac{5}{4}$,即$\frac{c}{a}=\sqrt{5}$.故选D.
(1)D
(1)不妨设$F(-c,0),B(0,b)$,则$M(-\frac{c}{2},\frac{b}{2})$.将点$M$坐标代入双曲线方程$\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1$,得$\frac{c^{2}}{4a^{2}}-\frac{1}{4}=1$,则$\frac{c^{2}}{4a^{2}}=\frac{5}{4}$,即$\frac{c}{a}=\sqrt{5}$.故选D.
(2)已知双曲线 $\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}} = 1(a > 0,b > 0)$,$ O $ 为坐标原点,$ F_{1} $,$ F_{2} $ 为其左、右焦点,若左支上存在一点 $ P $,使得 $ F_{2}P $ 的中点 $ M $ 满足 $ |OM| = \frac{1}{5}c $,则双曲线的离心率 $ e $ 的取值范围是
$(1,\frac{5}{3}]$
.
答案:
典例3
(2)$(1,\frac{5}{3}$
(2)因为$O,M$分别为$F_1F_2,PF_2$的中点,所以$|PF_1| = 2|OM|=\frac{2}{5}c$.
又双曲线上的点到焦点的最小距离为$c - a$,所以$\frac{2}{5}c\geqslant c - a>0$,解得$1<\frac{c}{a}\leqslant\frac{5}{3}$.因此双曲线的离心率$e$的取值范围是$(1,\frac{5}{3}$.
(2)$(1,\frac{5}{3}$
(2)因为$O,M$分别为$F_1F_2,PF_2$的中点,所以$|PF_1| = 2|OM|=\frac{2}{5}c$.
又双曲线上的点到焦点的最小距离为$c - a$,所以$\frac{2}{5}c\geqslant c - a>0$,解得$1<\frac{c}{a}\leqslant\frac{5}{3}$.因此双曲线的离心率$e$的取值范围是$(1,\frac{5}{3}$.
对点练 3 已知 $ A $,$ B $ 为双曲线 $ E $ 的左、右顶点,点 $ M $ 在双曲线 $ E $ 上,满足 $ \triangle ABM $ 为等腰三角形,顶角为 $ 120^{\circ} $,则双曲线 $ E $ 的离心率为( )
A.$\sqrt{2}$
B.$\sqrt{3}$
C.$ 2 $
D.$\sqrt{5}$
A.$\sqrt{2}$
B.$\sqrt{3}$
C.$ 2 $
D.$\sqrt{5}$
答案:
对点练3.A 不妨取点$M$在第一象限,如图所示.设双曲线的方程为$\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1(a>0,b>0)$,因为$\triangle ABM$
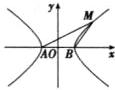
是顶角为$120^{\circ}$的等腰三角形,所以$|BM| = |AB| = 2a,\angle MBx = 60^{\circ}$,所以点$M$的坐标为$(2a,\sqrt{3}a)$.又因为点$M$在双曲线$\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1(a>0,b>0)$上,所以将点$M$坐标代入方程得$4-\frac{3a^{2}}{b^{2}} = 1$,整理上式得$a^{2}=b^{2}$.而$c^{2}=a^{2}+b^{2}=2a^{2}$,所以$e^{2}=2$,因此$e=\sqrt{2}$.故选A.
对点练3.A 不妨取点$M$在第一象限,如图所示.设双曲线的方程为$\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1(a>0,b>0)$,因为$\triangle ABM$

是顶角为$120^{\circ}$的等腰三角形,所以$|BM| = |AB| = 2a,\angle MBx = 60^{\circ}$,所以点$M$的坐标为$(2a,\sqrt{3}a)$.又因为点$M$在双曲线$\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1(a>0,b>0)$上,所以将点$M$坐标代入方程得$4-\frac{3a^{2}}{b^{2}} = 1$,整理上式得$a^{2}=b^{2}$.而$c^{2}=a^{2}+b^{2}=2a^{2}$,所以$e^{2}=2$,因此$e=\sqrt{2}$.故选A.
典例 4 双曲线 $\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}} = 1(a > 0,b > 0)$ 的一条渐近线经过点 $ (-1,-\sqrt{3}) $,则该双曲线的离心率为(
A.$\sqrt{5}$
B.$ 2 $
C.$\sqrt{3}$
D.$ 4 $
B
)A.$\sqrt{5}$
B.$ 2 $
C.$\sqrt{3}$
D.$ 4 $
答案:
典例4 B 易知双曲线的渐近线$y = \frac{b}{a}x$经过点$(-1,-\sqrt{3})$,将$(-1,-\sqrt{3})$代入渐近线方程得$\frac{b}{a}=\sqrt{3}$,所以$e = \sqrt{1+(\frac{b}{a})^{2}} = \sqrt{1 + 3}=2$.
故选B.
故选B.
对点练 4 已知双曲线 $ C:\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}} = 1(a > 0,b > 0)$ 的右顶点为 $ A $,左、右焦点分别为 $ F_{1} $,$ F_{2} $,渐近线在第一象限的部分上存在一点 $ P $,且 $ |OP| = |OF_{1}| $,直线 $ PF_{1} $ 的斜率为 $\frac{\sqrt{3}}{3}$,则该双曲线的离心率为
2
.
答案:
对点练4.2 由双曲线$C:\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1(a>0,b>0)$,可得渐近线方程为$y=\pm\frac{b}{a}x$,设点$P$的坐标为$(x_0,\frac{b}{a}x_0)$,且$x_0>0$,因为$|OP| = |OF_1|$,
即$x_0^{2}+\frac{b^{2}}{a^{2}}x_0^{2}=c^{2}$,解得$x_0^{2}=a^{2}$,即$x_0 = a$,所以点$P$的坐标为$(a,b)$,又
因为直线$PF_1$的斜率为$\frac{\sqrt{3}}{3}$,所以$\frac{b}{a + c}=\frac{\sqrt{3}}{3}$,可得$\sqrt{3}b = a + c$,两边平方得$3b^{2}=a^{2}+c^{2}+2ac$,即$c^{2}-ac - 2a^{2}=0$,两边同时除以$a^{2}$,可得$e^{2}-e - 2=0$,即$(e - 2)(e + 1)=0$,解得$e = 2$或$e=-1$(舍去).
即$x_0^{2}+\frac{b^{2}}{a^{2}}x_0^{2}=c^{2}$,解得$x_0^{2}=a^{2}$,即$x_0 = a$,所以点$P$的坐标为$(a,b)$,又
因为直线$PF_1$的斜率为$\frac{\sqrt{3}}{3}$,所以$\frac{b}{a + c}=\frac{\sqrt{3}}{3}$,可得$\sqrt{3}b = a + c$,两边平方得$3b^{2}=a^{2}+c^{2}+2ac$,即$c^{2}-ac - 2a^{2}=0$,两边同时除以$a^{2}$,可得$e^{2}-e - 2=0$,即$(e - 2)(e + 1)=0$,解得$e = 2$或$e=-1$(舍去).
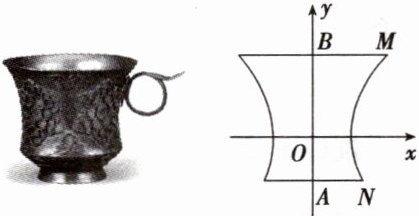
典例 5 如图为陕西历史博物馆收藏的国宝——唐·金筐宝钿团花纹金杯,杯身曲线内收,玲珑娇美,巧夺天工,是唐代金银细作的典范之作. 该杯的主体部分可以近似看作是双曲线 $ C:\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}} = 1(a > 0,b > 0)$ 的右支与 $ y $ 轴及平行于 $ x $ 轴的两条直线围成的曲边四边形 $ ABMN $ 绕 $ y $ 轴旋转一周得到的几何体. 若该金杯主体部分的上口外直径为 $\frac{10\sqrt{3}}{3}$,下底座外直径为 $\frac{2\sqrt{39}}{3}$,且杯身最细之处到上杯口的距离是到下底座距离的 $ 2 $ 倍,则杯身最细之处的周长为(
A.$ 2\sqrt{2}\pi $
B.$ 3\pi $
C.$ 2\sqrt{3}\pi $
D.$ 4\pi $
C
)
A.$ 2\sqrt{2}\pi $
B.$ 3\pi $
C.$ 2\sqrt{3}\pi $
D.$ 4\pi $
答案:
典例5 C 该金杯主体部分的上口外直径为$\frac{10\sqrt{3}}{3}$,下底座外直径为$\frac{2\sqrt{39}}{3}$,且杯身最细之处到上杯口的距离是到下底座距离的$2$倍,可设$M(\frac{5\sqrt{3}}{3},2m),N(\frac{\sqrt{39}}{3},-m)$,代入双曲线方程可得$\frac{25}{a^{2}}-\frac{4m^{2}}{b^{2}} = 1,\frac{13}{a^{2}}-\frac{m^{2}}{b^{2}} = 1$,即$\frac{25}{a^{2}}-\frac{4}{a^{2}}·\frac{3}{4}m^{2}=1,\frac{13}{a^{2}}-\frac{3}{4}·\frac{m^{2}}{b^{2}} = 1$,作差可得$\frac{12}{a^{2}}=\frac{3}{4}$,解得$a^{2}=3,a=\sqrt{3}$,所以杯身最细处的周长为$2\sqrt{3}\pi$.故选C.
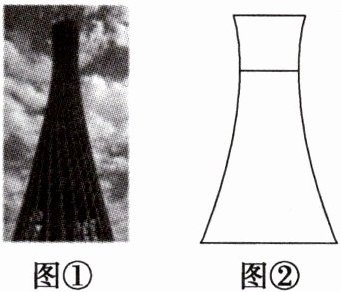
对点练 5 (新情境)单叶双曲面是最受设计师青睐的结构之一,它可以用直的钢梁建造,既能减少风的阻力,又能用最少的材料来维持结构的完整. 如图①,俗称小蛮腰的广州塔位于中国广州市,它的外形就是单叶双曲面,可看成是双曲线的一部分绕其虚轴旋转所形成的曲面. 某市计划建造类似于广州塔的地标建筑,此地标建筑的平面图形是双曲线,如图②,最细处的直径为 $ 100 \, m $,楼底的直径为 $ 50\sqrt{22} \, m $,楼顶直径为 $ 50\sqrt{6} \, m $,最细处距楼底 $ 300 \, m $,则该地标建筑的高为( )
A.$ 350 \, m $
B.$ 375 \, m $
C.$ 400 \, m $
D.$ 450 \, m $

A.$ 350 \, m $
B.$ 375 \, m $
C.$ 400 \, m $
D.$ 450 \, m $
答案:
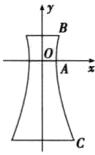
对点练5.C 以地标建筑的最细处所在直线为$x$轴,双曲线的虚轴为$y$轴,建立平面直角坐标系如图所示,由题意可得$A(50,0),C(25\sqrt{22},-300)$,设$B(25\sqrt{6},y_0)(y_0>0)$,双曲线的方程是$\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1(a>0,b>0)$,则
$\begin{cases}a = 50\frac{(25\sqrt{22})^{2}}{50^{2}}-\frac{(-300)^{2}}{b^{2}} = 1\end{cases}$
解得$\begin{cases}a = 50\\b = 100\sqrt{2}\end{cases}$
所以双曲线的方程是$\frac{x^{2}}{2500}-\frac{y^{2}}{20000}=1$,将点$B(25\sqrt{6},y_0)$代入得$\frac{25^{2}×6}{2500}-\frac{y_0^{2}}{20000}=1$,解得$y_0 = 100$,所以该地标建筑的高为$300 + 100 = 400(m)$.
故选C.
对点练5.C 以地标建筑的最细处所在直线为$x$轴,双曲线的虚轴为$y$轴,建立平面直角坐标系如图所示,由题意可得$A(50,0),C(25\sqrt{22},-300)$,设$B(25\sqrt{6},y_0)(y_0>0)$,双曲线的方程是$\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1(a>0,b>0)$,则
$\begin{cases}a = 50\frac{(25\sqrt{22})^{2}}{50^{2}}-\frac{(-300)^{2}}{b^{2}} = 1\end{cases}$
解得$\begin{cases}a = 50\\b = 100\sqrt{2}\end{cases}$
所以双曲线的方程是$\frac{x^{2}}{2500}-\frac{y^{2}}{20000}=1$,将点$B(25\sqrt{6},y_0)$代入得$\frac{25^{2}×6}{2500}-\frac{y_0^{2}}{20000}=1$,解得$y_0 = 100$,所以该地标建筑的高为$300 + 100 = 400(m)$.

故选C.
查看更多完整答案,请扫码查看


