2025年金版新学案高中数学选择性必修第一册北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年金版新学案高中数学选择性必修第一册北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第123页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
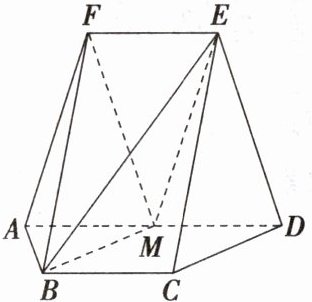
(2024·全国甲卷理)如图,在以$A$,$B$,$C$,$D$,$E$,$F$为顶点的五面体中,四边形$ABCD$与四边形$ADEF$均为等腰梯形,$EF// AD$,$BC// AD$,$AD = 4$,$AB = BC = EF = 2$,$ED = \sqrt{10}$,$FB = 2\sqrt{3}$,$M$为$AD$的中点。
(1)证明:$BM//$平面$CDE$;
(2)求二面角$F - BM - E$的正弦值。
溯源(北师版P142A组T22)
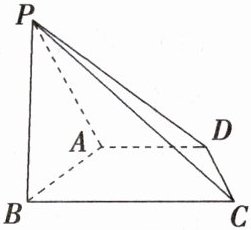
如图,在四棱锥$P - ABCD$中,底面$ABCD$为直角梯形,$\angle ABC = \angle BAD = \frac{\pi}{2}$,$PB\perp$平面$ABCD$,$PB = 5$,$AB = BC = 6$,$AD = 3$,求:
(1)点$B$到平面$PCD$的距离;
(2)二面角$P - CD - A$的平面角的余弦值。
点评
两题都是以底面为梯形的多面体为载体命制试题,都是考查空间想象能力、数学论证和计算能力。高考题整体难度高于教材题目,图中的数量关系较多、位置关系较复杂,需要思路清晰,条理清楚,要具有较强的空间想象能力。
(1)证明:$BM//$平面$CDE$;
(2)求二面角$F - BM - E$的正弦值。

溯源(北师版P142A组T22)
如图,在四棱锥$P - ABCD$中,底面$ABCD$为直角梯形,$\angle ABC = \angle BAD = \frac{\pi}{2}$,$PB\perp$平面$ABCD$,$PB = 5$,$AB = BC = 6$,$AD = 3$,求:
(1)点$B$到平面$PCD$的距离;
(2)二面角$P - CD - A$的平面角的余弦值。

点评
两题都是以底面为梯形的多面体为载体命制试题,都是考查空间想象能力、数学论证和计算能力。高考题整体难度高于教材题目,图中的数量关系较多、位置关系较复杂,需要思路清晰,条理清楚,要具有较强的空间想象能力。
答案:
(1) 证明见解析;
(2) 4√3/13。
(1) 证明见解析;
(2) 4√3/13。
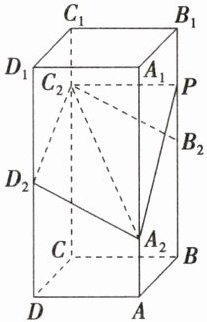
(2023·新课标Ⅰ卷)如图,在正四棱柱$ABCD - A_{1}B_{1}C_{1}D_{1}$中,$AB = 2$,$AA_{1} = 4$。点$A_{2}$,$B_{2}$,$C_{2}$,$D_{2}$分别在棱$AA_{1}$,$BB_{1}$,$CC_{1}$,$DD_{1}$上,$AA_{2} = 1$,$BB_{2} = DD_{2} = 2$,$CC_{2} = 3$。
(1)证明:$B_{2}C_{2}// A_{2}D_{2}$;
(2)点$P$在棱$BB_{1}$上,当二面角$P - A_{2}C_{2} - D_{2}$为$150^{\circ}$时,求$B_{2}P$。
溯源(北师版P142A组T20)
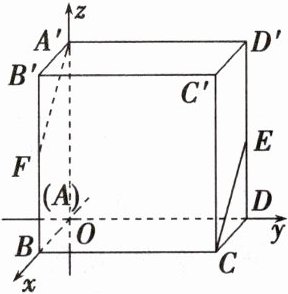
如图,在空间直角坐标系中有长方体$ABCD - A'B'C'D'$,$AB = 1$,$BC = 2$,$AA' = 2$,点$E$,$F$分别是棱$DD'$和$BB'$的中点。求证:$CE// A'F$,并求它们的距离。
点评
两题都是以四棱柱为载体命制试题,课本题目考查线线平行与线线距问题,而高考题考查线线平行与两点距问题,所以无论载体,还是考查内容及形式都极为相似,是很好的与教材有渊源的题目。两题都考查了空间想象能力、逻辑推理能力以及数学运算能力等核心素养。
(1)证明:$B_{2}C_{2}// A_{2}D_{2}$;
(2)点$P$在棱$BB_{1}$上,当二面角$P - A_{2}C_{2} - D_{2}$为$150^{\circ}$时,求$B_{2}P$。

溯源(北师版P142A组T20)
如图,在空间直角坐标系中有长方体$ABCD - A'B'C'D'$,$AB = 1$,$BC = 2$,$AA' = 2$,点$E$,$F$分别是棱$DD'$和$BB'$的中点。求证:$CE// A'F$,并求它们的距离。

点评
两题都是以四棱柱为载体命制试题,课本题目考查线线平行与线线距问题,而高考题考查线线平行与两点距问题,所以无论载体,还是考查内容及形式都极为相似,是很好的与教材有渊源的题目。两题都考查了空间想象能力、逻辑推理能力以及数学运算能力等核心素养。
答案:
(1) 证明见上;
(2) $B₂P=1$。
(1) 证明见上;
(2) $B₂P=1$。
(2023·新课标Ⅱ卷)如图,三棱锥$A - BCD$中,$DA = DB = DC$,$BD\perp CD$,$\angle ADB = \angle ADC = 60^{\circ}$,$E$为$BC$的中点。
(1)证明:$BC\perp DA$;
(2)点$F$满足$\overrightarrow{EF}=\overrightarrow{DA}$,求二面角$D - AB - F$的正弦值。

溯源(北师版P141A组T18)
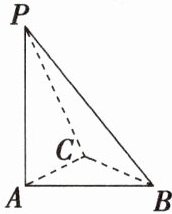
如图,在三棱锥$P - ABC$中,已知$PA\perp$平面$ABC$,$AC\perp BC$,$CA = CB = 2$,$PA = 2\sqrt{3}$,求二面角$A - BC - P$的平面角。
点评
两题都是以三棱锥为载体考查二面角等问题。高考题是双问形式设计,尽管与教材题目有关联,但难度明显高于教材。对于高考题中的立体几何来说,建立合理的空间直角坐标系是一项基本的技能和能力,同时还要注重表达的严谨性和推理的合理性。
(1)证明:$BC\perp DA$;
(2)点$F$满足$\overrightarrow{EF}=\overrightarrow{DA}$,求二面角$D - AB - F$的正弦值。

溯源(北师版P141A组T18)
如图,在三棱锥$P - ABC$中,已知$PA\perp$平面$ABC$,$AC\perp BC$,$CA = CB = 2$,$PA = 2\sqrt{3}$,求二面角$A - BC - P$的平面角。

点评
两题都是以三棱锥为载体考查二面角等问题。高考题是双问形式设计,尽管与教材题目有关联,但难度明显高于教材。对于高考题中的立体几何来说,建立合理的空间直角坐标系是一项基本的技能和能力,同时还要注重表达的严谨性和推理的合理性。
答案:
(1) 证明:设 $ DA = DB = DC = a $。
在 $ \triangle ADB $ 中,由余弦定理得 $ AB^2 = a^2 + a^2 - 2a^2\cos60° = a^2 $,故 $ AB = a $。同理 $ AC = a $。
因 $ BD \perp CD $,则 $ BC^2 = a^2 + a^2 = 2a^2 $,即 $ BC = \sqrt{2}a $。
在 $ \triangle ABC $ 中,$ AB^2 + AC^2 = a^2 + a^2 = 2a^2 = BC^2 $,故 $ AB \perp AC $。
取 $ BC $ 中点 $ E $,连接 $ AE $,$ DE $。由 $ AB = AC $ 得 $ AE \perp BC $,由 $ DB = DC $ 得 $ DE \perp BC $。
因 $ AE \cap DE = E $,则 $ BC \perp $ 平面 $ ADE $,又 $ DA \subset $ 平面 $ ADE $,故 $ BC \perp DA $。
(2) 解:以 $ D $ 为原点,$ DC $,$ DB $ 为 $ x $,$ y $ 轴,建立空间直角坐标系,设 $ DA = DB = DC = 2 $。
则 $ D(0,0,0) $,$ C(2,0,0) $,$ B(0,2,0) $,由 $ \angle ADB = \angle ADC = 60° $ 得 $ A(1,1,\sqrt{2}) $,$ E(1,1,0) $。
由 $ \overrightarrow{EF} = \overrightarrow{DA} = (1,1,\sqrt{2}) $,得 $ F(2,2,\sqrt{2}) $。
平面 $ DAB $ 法向量 $ \boldsymbol{n} = (-\sqrt{2},0,1) $,平面 $ ABF $ 法向量 $ \boldsymbol{m} = (1,-1,-\sqrt{2}) $。
$ |\cos\theta| = \frac{|\boldsymbol{n} · \boldsymbol{m}|}{|\boldsymbol{n}||\boldsymbol{m}|} = \frac{2\sqrt{2}}{\sqrt{3} × 2} = \frac{\sqrt{6}}{3} $,故 $ \sin\theta = \sqrt{1 - (\frac{\sqrt{6}}{3})^2} = \frac{\sqrt{3}}{3} $。
(1) 证明:设 $ DA = DB = DC = a $。
在 $ \triangle ADB $ 中,由余弦定理得 $ AB^2 = a^2 + a^2 - 2a^2\cos60° = a^2 $,故 $ AB = a $。同理 $ AC = a $。
因 $ BD \perp CD $,则 $ BC^2 = a^2 + a^2 = 2a^2 $,即 $ BC = \sqrt{2}a $。
在 $ \triangle ABC $ 中,$ AB^2 + AC^2 = a^2 + a^2 = 2a^2 = BC^2 $,故 $ AB \perp AC $。
取 $ BC $ 中点 $ E $,连接 $ AE $,$ DE $。由 $ AB = AC $ 得 $ AE \perp BC $,由 $ DB = DC $ 得 $ DE \perp BC $。
因 $ AE \cap DE = E $,则 $ BC \perp $ 平面 $ ADE $,又 $ DA \subset $ 平面 $ ADE $,故 $ BC \perp DA $。
(2) 解:以 $ D $ 为原点,$ DC $,$ DB $ 为 $ x $,$ y $ 轴,建立空间直角坐标系,设 $ DA = DB = DC = 2 $。
则 $ D(0,0,0) $,$ C(2,0,0) $,$ B(0,2,0) $,由 $ \angle ADB = \angle ADC = 60° $ 得 $ A(1,1,\sqrt{2}) $,$ E(1,1,0) $。
由 $ \overrightarrow{EF} = \overrightarrow{DA} = (1,1,\sqrt{2}) $,得 $ F(2,2,\sqrt{2}) $。
平面 $ DAB $ 法向量 $ \boldsymbol{n} = (-\sqrt{2},0,1) $,平面 $ ABF $ 法向量 $ \boldsymbol{m} = (1,-1,-\sqrt{2}) $。
$ |\cos\theta| = \frac{|\boldsymbol{n} · \boldsymbol{m}|}{|\boldsymbol{n}||\boldsymbol{m}|} = \frac{2\sqrt{2}}{\sqrt{3} × 2} = \frac{\sqrt{6}}{3} $,故 $ \sin\theta = \sqrt{1 - (\frac{\sqrt{6}}{3})^2} = \frac{\sqrt{3}}{3} $。
查看更多完整答案,请扫码查看


