第68页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
9. 如图1所示,搭1个三角形需要6根火柴棒,搭2个三角形需要10根火柴棒;如图2所示,搭1个五边形需要5根火柴棒,搭2个五边形需要9根火柴棒;按图1、图2的方法搭2026个三角形比搭2025个五边形所用的火柴棒的根数多(

A.1根
B.5根
C.2025根
D.2026根
B
)
A.1根
B.5根
C.2025根
D.2026根
答案:
9. B 解析:探索规律发现,搭2026个三角形需火柴棒$(2 + 4×2026)$根;搭2025个五边形则需火柴棒$(1 + 4×2025)$根。求差得$2 + 4×2026 - (1 + 4×2025) = 1 + 4 = 5$(根)。故选B。
10. 已知8个长为$a$,宽为$b$的小长方形(如图1所示),不重叠无空隙地摆放(如图2所示)在长方形$ABCD$中,$BC$长度变化时,左上角阴影面积$S_{1}$与右下角阴影面积$S_{2}$的差没有变化,则$a,b$之间的关系应满足(
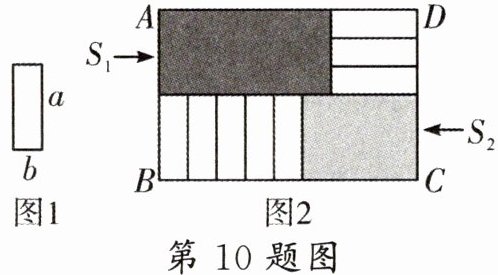
A.$5b = 2a$
B.$3b = a$
C.$2b = a$
D.$5b = 3a$
B
)
A.$5b = 2a$
B.$3b = a$
C.$2b = a$
D.$5b = 3a$
答案:
10. B 解析:$S_1 - S_2 = 3b(BC - a) - a(BC - 5b) = (3b - a)BC + 2ab$,要使$S_1$与$S_2$的差不变,则$3b - a = 0$。
故选B。
故选B。
11. 计算$-7x + 3x=$
-4x
。
答案:
11. $-4x$
12. $m$是1个三位数,$n$是1个一位数,把$m$写到$n$的左边得到1个四位数,用含$m,n$的一次式表示这个四位数为
10m + n
。
答案:
12. $10m + n$
13. 如图,数轴上的点$A$所表示的数为$a$,化简$\vert a\vert-\vert 1 - a\vert=$
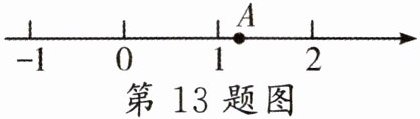
1
。
答案:
13. 1
14. 学校田径队进行跑步测试,小刚先以$6m/s$的平均速度跑了$m$秒,然后以$8m/s$的平均速度冲刺到达终点,成绩为$65s$,则小刚的跑步测试距离是
-2m + 520
$m$(用含$m$的代数式表示)。
答案:
14. $(-2m + 520)$
15. 把有理数$a$代入$\vert a + 2\vert-10$得到$a_{1}$,称为第1次操作,再将$a_{1}$作为$a$的值代入得到$a_{2}$,称为第2次操作,依此类推,若$a = 22$,则经过第2025次操作后得到的是
-2
。
答案:
15. $-2$ 解析:由题意得$a_1 = |22 + 2| - 10 = 14$;$a_2 = |14 + 2| - 10 = 6$;$a_3 = |6 + 2| - 10 = -2$;$a_4 = |-2 + 2| - 10 = -10$;$a_5 = |-10 + 2| - 10 = -2$;$a_6 = |-2 + 2| - 10 = -10$;$\cdots$;观察到第2次以后的奇数次操作结果均为$-2$,偶数次操作均为$-10$,故$a_{2025} = -2$。
16. 已知$ax^{3}+bx^{2}+cx + d = (\frac{1}{2}x - 1)^{3}$,当$x = 1$时,左式$=a + b + c + d$,右式$=-\frac{1}{8}$,所以有$a + b + c + d = -\frac{1}{8}$;那么如果$x = -1\cdots\cdots$
(1)$a - b + c - d=$
(2)$8a + 4b + 2c + d=$
(1)$a - b + c - d=$
27/8
。(2)$8a + 4b + 2c + d=$
0
。
答案:
16.
(1)$\frac{27}{8}$
(2)0
(1)$\frac{27}{8}$
(2)0
查看更多完整答案,请扫码查看


