《2025年初中全程阶段测评卷七年级数学上册浙教版》

11. 如图，已知点$B$在线段$AC$上，点$D$在线段$AB$上，若$AB = 6cm$，$DC = 5cm$，$AC = 10cm$。
（1）求线段$DB$的长度。
（2）若$E$为线段$AB$的中点，求线段$DE$的长度。

答案： 11.
(1)因为$AB=AD+DB$，$DC=DB+BC$，$AC=AD+DB+BC$，所以$DB=AB+DC - AC=6+5 - 10=1(cm)$。
(2)因为$AB=6cm$，E为AB中点，所以$BE=3cm$，又因为$DB=1cm$，所以$DE=2cm$。

12. 如图，点$O$在直线$AB$上，$∠BOD$与$∠COD$互补，$∠BOC = n∠EOC$。
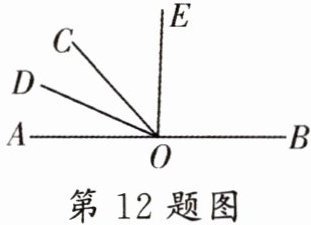
（1）若$∠AOD = 24^{\circ}$，$n = 3$，求$∠DOE$的度数。
（2）若$∠DOE = 90^{\circ}$，求$n$的值。
（3）若$n = 4$，设$∠AOD = α$，求$∠DOE$的度数（用含$α$的代数式表示$∠DOE$的度数）。

答案： 12.
(1)因为$\angle BOD$与$\angle COD$互补，所以$\angle BOD+\angle COD=180^{\circ}$，又因为$\angle BOD+\angle AOD=180^{\circ}$，所以$\angle AOD=\angle COD$。因为$\angle AOD=24^{\circ}$，所以$\angle BOC=180^{\circ}-\angle AOD-\angle COD=132^{\circ}$，因为$\angle BOC=3\angle EOC$，所以$\angle EOC=44^{\circ}$，所以$\angle DOE=\angle DOC+\angle COE=24^{\circ}+44^{\circ}=68^{\circ}$。
(2)设$\angle AOD=x$。因为$\angle BOD+\angle AOD=180^{\circ}$，$\angle BOD+\angle COD=180^{\circ}$，所以$\angle AOD=\angle COD=x$，所以$\angle AOC=\angle AOD+\angle COD=2x$，所以$\angle BOC=180^{\circ}-\angle AOC=180^{\circ}-2x$。因为$\angle DOE=90^{\circ}$，所以$\angle COE=90^{\circ}-\angle COD=90^{\circ}-x$。因为$\angle BOC=n\angle EOC$，所以$180^{\circ}-2x=n(90^{\circ}-x)$，$n=2$。
(3)因为$\angle BOD+\angle AOD=180^{\circ}$，$\angle BOD+\angle COD=180^{\circ}$，所以$\angle AOD=\angle COD=\alpha$，所以$\angle BOC=180^{\circ}-2\alpha$。因为$n=4$，所以$4\angle EOC=180^{\circ}-2\alpha$，所以$\angle EOC=\frac{1}{4}×(180^{\circ}-2\alpha)=45^{\circ}-\frac{1}{2}\alpha$，所以$\angle EOD=\angle COD+\angle EOC=45^{\circ}-\frac{1}{2}\alpha+\alpha=45^{\circ}+\frac{\alpha}{2}$。