《2025年初中全程阶段测评卷七年级数学上册浙教版》

8. 若$mn≠0$，则$\frac{|m|}{m}+\frac{|n|}{n}$的值不可能是(B)

A.0
B.1
C.2
D.$-2$

答案： 8.B

9. 如图，在这个数据运算程序中，若开始输入的x的值为4，输出的结果是2，返回进行第2次运算则输出的是1……则第2025次输出的结果是(C)

A.$-1$
B.$-8$
C.$-4$
D.$-6$

答案： 9.C

10. 设a，b是有理数，定义关于“*”的一种运算为$a*b=2a+2b$，则下列结论中：①若$a*b=0$，则a，b互为相反数；②$a*b=b*a$；③$a*(b+c)=a*b+a*c$；④若$a*b=8$，则$3-2a-2b=-5$。正确的有(C)

A.①②
B.①②③
C.①②④
D.①②③④

答案： 10.C 解析：因为 a * b = 2a + 2b,a * b = 0，所以 2a + 2b = 0，所以 a + b = 0，所以 a,b 互为相反数，所以①正确。 因为 a * b = 2a + 2b,b * a = 2b + 2a，所以 a * b = b * a，所以②正确。 因为 a * (b + c) = 2a + 2(b + c) = 2a + 2b + 2c,a * b + a * c = 2a + 2b + 2a + 2c = 4a + 2b + 2c，所以 a * (b + c) ≠ a * b + a * c，所以③不正确。
因为 a * b = 8,a * b = 2a + 2b，所以 2a + 2b = 8，所以 -2a - 2b = -8，所以 3 - 2a - 2b = 3 - 8 = -5，
所以④正确。 故选 C。

11. 某市某天的最高气温是8℃，最低气温是-3℃，那么这天的温差是11℃。

答案： 11.11

12. 计算$-8+10-3=$-1。

答案： 12.-1

13. 某检修小组从A地出发，在东西方向的马路上检修线路，若规定向东行驶为正，向西行驶为负，一天中5次行驶记录如下(单位：km)：+7，-9，+8，-6，-5，则收工时检修小组在A地西边5km。

答案： 13.西 5

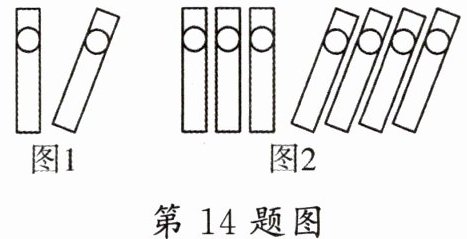
14. 中国人最先使用负数，魏晋时期的数学家刘徽在“正负术”的注文中指出，可将算筹(小棍形状的记数工具)正放表示正数，斜放表示负数，根据刘徽的这种表示法，图1表示的数值为$(+1)+(-1)=0$，则可推算图2表示的数值是-1(直接写出结果)。

答案： 14.-1

15. 若$(a+3)^2+|b-2|=0$，则$a^b=$9。

答案： 15.9 解析：由非负数性质知$\begin{cases}a + 3 = 0, \\b - 2 = 0.\end{cases}$解得 a = -3，
b = 2，故$a^b = (-3)^2 = 9$。

16. 在学习了有理数的运算后，小明定义了新的运算：取大运算“∨”和取小运算“∧”，如$3∨2=3$，$3∧2=2$。利用“加、减、乘、除”以及新运算法则进行运算，下列运算中正确的是②③。
①$[3∨(-2)]∧4=4$；②$(a∨b)∨c=a∨(b∨c)$；③$-(a∨b)=(-a)∧(-b)$；④$(a∧b)×c=ac∧bc$。

答案： 16.②③ 解析：①因为$[3V(-2)]Δ4 = 3Δ4 = 3 ≠ 4$，所以①不正确。 ②因为$(aVb)Vc = \max\{a,b,c\},aV(bVc) = \max\{a,b,c\}$，所以$(aVb)Vc = aV(bVc)$，所以②正确。
③因为$-(aVb) = -\max\{a,b\} = \min\{-a,-b\}$，$(-a)Δ(-b) = \min\{-a,-b\}$，所以$-(aVb) = (-a)Δ(-b)$，所以③正确。 ④因为若取 a = 2,b = -2,c = -3，则有$(aΔb)×c = -2×(-3) = 6,acΔbc = -6Δ6 = -6$，所以$(aΔb)×c ≠ acΔbc$，所以④不正确。
故答案为②③。