《2025年课堂点睛九年级数学上册人教版安徽专版》

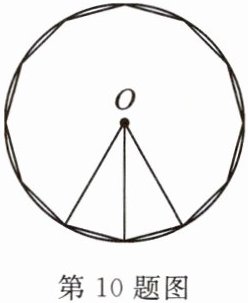
10. (数学文化)刘徽是我国魏晋时期卓越的数学家,他在《九章算术》中提出了“割圆术”,利用圆的内接正多边形逐步逼近圆来近似计算圆的面积. 如图,若用圆的内接正十二边形的面积$S_1$来近似估计⊙O的面积S,设⊙O的半径为1,则$S - S_1 = $0.14. (π取3.14)

答案： 0.14

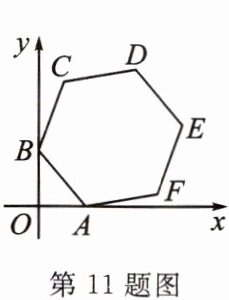
11. 如图,正六边形ABCDEF的边长为4,两顶点A、B分别在x轴和y轴上运动,则顶点D到x轴的距离的最大值为8.

答案： 8

12. (原创题)如图,等边三角形ABC外切于⊙O,正方形DEFG内接于⊙O,若等边三角形ABC的边长为6,求正方形DEFG的边长.

答案： 解:设⊙O与BC相切于点M,连接OC,OM,则OM⊥BC.
∵⊙O是等边三角形ABC的内切圆,
∴CO平分∠ACB,
∴∠OCM=30°,
∴OC=2OM,
∴在Rt△OMC中,设OM=r,得r²+CM²=OC²,r²+CM²=4r²,3r²=CM²,又
∵BC=6,
∴CM=3,
∴3r²=9,r=$\sqrt{3}$,
∴连接OG,OD后,由正方形DEFG可得∠DOG=90°,
∴DG²=r²+r²,
∴DG=$\sqrt{2}$r=$\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$.

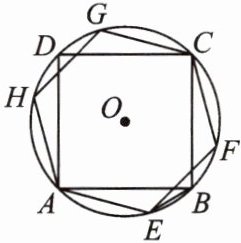
13. 如图,⊙O是正方形ABCD与正六边形AEFCGH的外接圆.
(1) 正方形ABCD与正六边形AEFCGH的边长之比为$\sqrt{2}$:1；
(2) 连接BE,BE是否为⊙O的内接正n边形的一边？如果是,求出n的值；如果不是,请说明理由.

(2)解:BE是⊙O的内接正十二边形的一边,理由如下:连接OA,OB,OE.在正方形ABCD中,∠AOB=$\frac{360°}{4}$=90°.在正六边形AEFCGH中,∠AOE=$\frac{360°}{6}$=60°.
∴∠BOE=∠AOB-∠AOE=30°.
∵$\frac{360°}{30°}$=12,
∴BE是⊙O的内接正十二边形的一边.

答案：
(1)$\sqrt{2}$:1
(2)解:BE是⊙O的内接正十二边形的一边,理由如下:连接OA,OB,OE.在正方形ABCD中,∠AOB=$\frac{360°}{4}$=90°.在正六边形AEFCGH中,∠AOE=$\frac{360°}{6}$=60°.
∴∠BOE=∠AOB-∠AOE=30°.
∵$\frac{360°}{30°}$=12,
∴BE是⊙O的内接正十二边形的一边.

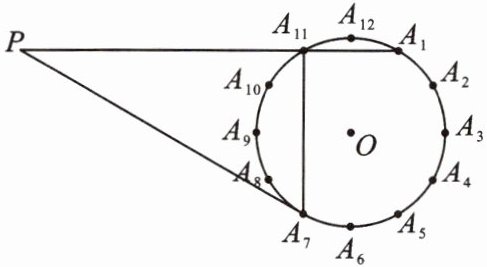
14. (核心素养·抽象能力)如图,⊙O的半径为6,将该圆周12等分后得到表盘模型,其中整钟点为Aₙ(n为1～12的整数),过点$A_7$作⊙O的切线交$A_1A_1_1$的延长线于点P.
(1) 连接$A_7A_1_1,$则$A_7A_1_1$和$PA_1$有什么特殊位置关系？请简要说明理由；
(2) 求切线长$PA_7$的值.

答案：
(1)解:A₇A₁₁⊥PA₁,理由如下:连接A₁A₇,
∵线段A₇A₁为⊙O的直径,
∴∠A₇A₁₁A₁=90°,
∴A₇A₁₁⊥PA₁.
(2)连接A₁₁O,
∵圆周被12等分,
∴∠A₁₁OA₁=60°,又
∵OA₁₁=OA₁,
∴△A₁₁OA₁为等边三角形,
∴∠A₁₁A₁O=60°,
∵PA₇为⊙O的切线,
∴∠PA₇A₁=90°,
∴切线长PA₇=$\sqrt{3}$A₇A₁=12$\sqrt{3}$.