《2025年课堂点睛九年级数学上册人教版安徽专版》

1. 某鞋帽专卖店销售一种绒帽. 若这种帽子每天获利 $ y $ (元) 与销售单价 $ x $ (元) 满足关系式 $ y = -x^{2} + 70x - 800 $,要想获得最大利润,则销售单价为(B)
A.30 元
B.35 元
C.40 元
D.45 元

答案： B

2. (聊城市中考) 某食品零售店新上架一款冷饮产品,每个成本为 8 元,在销售过程中,每天的销售量 $ y $ (个) 与销售价格 $ x $ (元/个) 的关系如图所示,当 $ 10 \leq x \leq 20 $ 时,其图象是线段 $ AB $,则该食品零售店每天销售这款冷饮产品的最大利润为121元 (利润 = 总销售额 - 总成本).

答案： 121

3. 某体育用品店购进一批单价为 20 元的球服,如果按单价 40 元销售,那么一个月内可售出 200 套,根据销售经验,提高销售单价会导致销量的减少,即销售单价每提高 4 元,销售量相应减少 20 套. 设销售单价为 $ x $ ($ x \geq 40 $) 元,销售量为 $ y $ 套.
(1) 求出 $ y $ 与 $ x $ 的函数关系式,并写出自变量取值范围；
(2) 当销售单价为多少元时,才能在一个月内获得最大利润？最大利润是多少？

答案：
(1)解:y=200-$\frac{x-40}{4}$×20=400-5x,自变量的取值范围是 40≤x≤80.
(2)设一个月的利润为 w 元,则 w=(400-5x)(x-20)=-5x²+500x-8000=-5(x-50)²+4500.
∵-5＜0,40≤x≤80,
∴当 x=50 时,w 有最大值,最大值是 4500.答:当销售单价为 50 元时,才能在一个月内获得最大利润,最大利润是 4500 元.

4. 某科技公司销售高新科技产品,该产品成本为 8 万元,销售单价 $ x $ (万元) 与销售量 $ y $ (件) 的关系如下表所示：

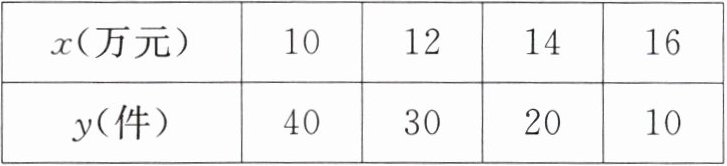
(1) 求 $ y $ 与 $ x $ 的函数关系式；
(2) 当销售单价为多少时,有最大利润,最大利润为多少？

答案：
(1)解:由表可知 y 是 x 的一次函数,设 y=kx+b,将(10,40),(12,30)代入,得$\left\{\begin{array}{l} 10k+b=40,\\ 12k+b=30,\end{array}\right. $解得$\left\{\begin{array}{l} k=-5,\\ b=90,\end{array}\right. $
∴y 与 x 的函数关系式为 y=-5x+90.
(2)设销售总利润为 w 万元.根据题意,得 w=(x-8)·y=(x-8)(-5x+90).即 w=-5x²+130x-720=-5(x-13)²+125.
∵a=-5＜0,
∴当 x=13 时,有最大利润,w${}_{最大}$=125.答:当销售单价为 13 万元时,有最大利润,最大利润为 125 万元.

5. 某商品的利润 $ y $ (元) 与售价 $ x $ (元) 之间的函数解析式是 $ y = -x^{2} + 8x + 9 $,且售价 $ x $ 的范围是 $ 1 \leq x \leq 3 $,则最大利润是(C)
A.16 元
B.21 元
C.24 元
D.25 元

答案： C

6. (原创题) 某电商平台 11 月 1 日起开始销售一款新品牌手机,当月的日销售额 $ y $ (万元) 和销售时间第 $ x $ 天 ($ 1 \leq x \leq 30 $,且 $ x $ 为整数) 之间满足二次函数关系 $ y = -(x - h)^{2} + k $,根据市场调查可以确定在当月中旬日销售额达到最大值. 若第 18 天的销售额比第 19 天的销售额多 5 万元,则第16天的日销售额最大.

答案： 16