《2025年课堂点睛九年级数学上册人教版安徽专版》

9. (原创题)如图,△ABC中,∠BAC= 50°,将△ABC绕点A逆时针旋转70°得到△AB'C',连接BB',BC'.若AC'= BC',则∠B'BC'的度数为35°.

答案： 35°

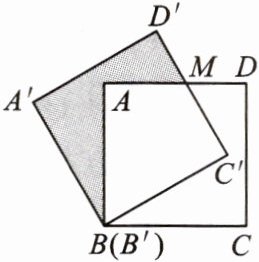
10. 如图,将边长为$\sqrt{3}$的正方形绕点B逆时针旋转30°,那么图中阴影部分的面积为$3-\sqrt{3}$.

答案： $3-\sqrt{3}$

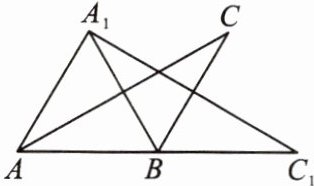
11. 如图,将一个钝角三角形ABC(其中∠ABC= 120°)绕点B顺时针旋转得$△A_1BC_1,$使得点C落在AB的延长线上的点$C_1$处,连接$AA_1.$
(1)直接写出旋转角的度数；
(2)求证：$∠A_1AC= ∠C_1.$

答案：
(1)解:旋转角的度数为60°.
(2)证明:
∵点A,B,C₁在一条直线上,
∴∠ABC₁=180°.
∵∠ABC=∠A₁BC₁=120°,
∴∠ABA₁=∠CBC₁=60°.
∴∠A₁BC=60°.又
∵AB=A₁B,
∴△ABA₁是等边三角形.
∴∠AA₁B=∠A₁BC=60°.
∴AA₁//BC.
∴∠A₁AC=∠C.
∵△ABC≌△A₁BC₁,
∴∠C=∠C₁.
∴∠A₁AC=∠C₁.

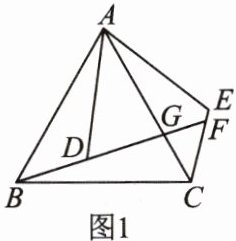
12. (核心素养·几何直观)如图1,D为等边三角形ABC内一点,将线段AD绕点A逆时针旋转60°得到AE,连接CE,BD的延长线与AC交于点G,与CE交于点F.
(1)求证：BD= CE；
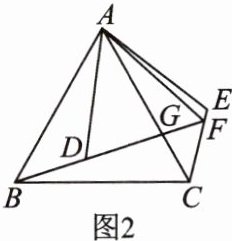
(2)如图2,连接FA,小颖对该图形进行探究,得出结论：∠BFC= ∠AFB= ∠AFE.小颖的结论是否正确？若正确,请给出证明；若不正确,请说明理由.

答案：
(1)证明:
∵线段AD绕点A逆时针旋转60°得到AE,
∴AD=AE,∠DAE=60°.
∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°.
∴∠BAC=∠DAE.
∴∠BAD=∠CAE.在△ABD和△ACE中,$\left\{\begin{array}{l} AB=AC,\\ ∠BAD=∠CAE,\\ AD=AE,\end{array}\right. $
∴△ABD≌△ACE(SAS).
∴BD=CE.
(2)解:正确.证明如下:
∵△ABD≌△ACE,
∴∠ABD=∠ACE.又
∵∠AGB=∠CGF,
∴∠BFC=∠BAC=60°.
∴∠BFE=120°.过点A作BD,CF的垂线段,垂足分别为M,N,
∵△ABD≌△ACE,BD=CE,
∴$\frac{1}{2}BD·AM=\frac{1}{2}CE·AN$,即AM=AN.
∴∠AFM=∠AFN=$\frac{1}{2}∠BFE$=60°.
∴∠BFC=∠AFB=∠AFE.