第18页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
8. 宾馆有 50 间房供游客居住,当每间房每天定价为 180 元时,宾馆会住满;当每间房每天的定价每增加 10 元时,就会空闲一间房。如果有游客居住,宾馆需对居住的每间房每天支出 20 元的费用。当房价定为多少元时,宾馆当天的利润为 10890 元?设房价定为 x 元,则有(
A.$(180 + x - 20)(50 - \frac{x}{10}) = 10890$
B.$(x - 20)(50 - \frac{x - 180}{10}) = 10890$
C.$x(50 - \frac{x - 180}{10}) - 50×20 = 10890$
D.$(x + 180)(50 - \frac{x}{10}) - 50×20 = 10890$
B
)A.$(180 + x - 20)(50 - \frac{x}{10}) = 10890$
B.$(x - 20)(50 - \frac{x - 180}{10}) = 10890$
C.$x(50 - \frac{x - 180}{10}) - 50×20 = 10890$
D.$(x + 180)(50 - \frac{x}{10}) - 50×20 = 10890$
答案:
B
9. 如图,育才中学要在宽为 20 米、长为 32 米的矩形地面上修筑同样宽的道路(图中阴影部分),余下部分种植草坪,要使草坪的面积为 540 平方米,则道路的宽为(
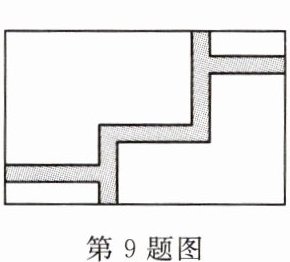
A.5 米
B.3 米
C.2 米
D.2 米或 5 米
C
)
A.5 米
B.3 米
C.2 米
D.2 米或 5 米
答案:
C
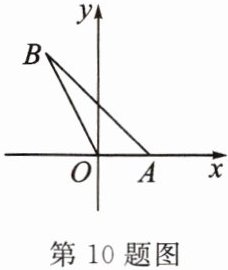
10. (原创题)如图,由点 $A(a, 0)$,$O(0, 0)$,$B(-a, a + 3)(a > 0)$确定的 $\triangle AOB$ 的面积为 2,则 a 的值为
1
。
答案:
1
11. 某商店购进 600 个旅游纪念品,进价为每个 6 元,第一周以每个 10 元的价格售出 200 个,第二周若按每个 10 元的价格销售,仍可售出 200 个。但商店为了适当增加销量,决定降价销售(根据市场调查,单价每降低 1 元,可多售出 50 个,但售价不得低于进价),单价降低 x 元销售一周后,商店对剩余旅游纪念品进行清仓处理,以每个 4 元的价格全部售出。如果这批旅游纪念品共获利 1250 元,那么第二周每个旅游纪念品的销售价格为多少元?
答案:
解:由题意,得200×(10−6)+(10−x−6)(200+50x)+(4 −6)×[600−200−(200+50x)]=1250,即800+(4−x)(200+50x)−2(200−50x)=1250,整理,得x²−2x+1=0,解得x₁=x₂=1,且符合题意,则第二周的销售价格为10−1=9(元).答:第二周每个旅游纪念品的销售价格为9元.
12. (核心素养·运算能力)如图,现打算用 60m 的篱笆围成一个“日”字形花园 ABCD(含隔离栏 EF),花园的一面靠墙 MN,墙 MN 可利用的长度为 25m。(篱笆的宽度忽略不计)

(1)花园的面积可能是$ 252m^2$吗?若可能,求边 AB 的长;若不可能,说明理由;
(2)花园的面积可能是$ 330m^2$吗?若可能,求边 AB 的长;若不可能,说明理由。

(1)花园的面积可能是$ 252m^2$吗?若可能,求边 AB 的长;若不可能,说明理由;
(2)花园的面积可能是$ 330m^2$吗?若可能,求边 AB 的长;若不可能,说明理由。
答案:
解:设AB的长为xm,则BC的长为(60−3x)m.
(1)可能.由题意,得x(60−3x)=252,解得x=6或x=14,当x=6时,BC=60−18=42>25,舍去;当x=14时,BC=60−42=18<25,满足题意,则花园的面积可能是252m²,此时边AB的长为14m.
(2)不可能.理由:由题意,得x(60−3x)=330,整理,得(x−10)²=−10,即方程没有实数根,则花园的面积不可能是330m².
(1)可能.由题意,得x(60−3x)=252,解得x=6或x=14,当x=6时,BC=60−18=42>25,舍去;当x=14时,BC=60−42=18<25,满足题意,则花园的面积可能是252m²,此时边AB的长为14m.
(2)不可能.理由:由题意,得x(60−3x)=330,整理,得(x−10)²=−10,即方程没有实数根,则花园的面积不可能是330m².
查看更多完整答案,请扫码查看


