第43页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
1. (北京市中考改编)如图,用绳子围成周长为 10m 的矩形,记矩形的一边长为 xm,它的邻边长为 ym,矩形的面积为$ Sm^2。$当 x 在一定范围内变化时,y 和 S 都随 x 的变化而变化,则 S 与 x 满足的函数关系式为(

A.$ S = x(5 - x)(0 < x < 5) $
B.$ S = x(10 - x)(0 < x < 5) $
C.$ S = x(x - 5)(0 < x < 5) $
D.$ S = x(x - 10)(0 < x < 5) $
A
)
A.$ S = x(5 - x)(0 < x < 5) $
B.$ S = x(10 - x)(0 < x < 5) $
C.$ S = x(x - 5)(0 < x < 5) $
D.$ S = x(x - 10)(0 < x < 5) $
答案:
A
2. 如图,利用一个直角墙角修建一个梯形储料场 ABCD,其中 $ ∠C = 120^{\circ} $。若新建墙 BC 与 CD 总长为 12m,则该梯形储料场 ABCD 的最大面积是(
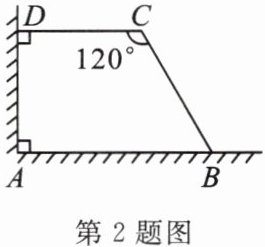
$A.18m^2$
B.$ 18\sqrt{3}m^{2} $
C.$ 24\sqrt{3}m^{2} $
D.$ \frac{45\sqrt{3}}{2}m^{2} $
C
)
$A.18m^2$
B.$ 18\sqrt{3}m^{2} $
C.$ 24\sqrt{3}m^{2} $
D.$ \frac{45\sqrt{3}}{2}m^{2} $
答案:
C
3. (教材第 52 页第 5 题变式)如图,四边形 ABCD 的两条对角线互相垂直,$ AC + BD = 16 $,则四边形 ABCD 的面积最大值是(
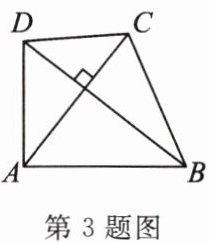
A.16
B.32
C.36
D.64
B
)
A.16
B.32
C.36
D.64
答案:
B
4. 如图,用一段长为 16m 的篱笆围成一个一边靠墙的矩形围栏(墙足够长),则这个围栏的最大面积为

32
$m^2。$
答案:
32
5. 如图,已知 $ □ABCD $ 的周长为 8cm,$ ∠B = 30^{\circ} $,若边长 $ AB = xcm $,过点 A 作 $ AE ⊥ BC $ 于点 E。
(1) $ AE = $
(2) $ □ABCD $ 的面积 $ y(cm^{2}) $ 与 x 之间的函数解析式为
(3) 当 x 取

(1) $ AE = $
$\frac{1}{2}x$
(用含 x 的代数式表示);(2) $ □ABCD $ 的面积 $ y(cm^{2}) $ 与 x 之间的函数解析式为
$y=-\frac{1}{2}x^{2}+2x$
,自变量 x 的取值范围为$0<x<4$
;(3) 当 x 取
2
时,y 的值最大,最大值为2
。
答案:
(1)$\frac{1}{2}x$
(2)$y=-\frac{1}{2}x^{2}+2x$ $0<x<4$
(3)2 2
(1)$\frac{1}{2}x$
(2)$y=-\frac{1}{2}x^{2}+2x$ $0<x<4$
(3)2 2
6. 已知直角三角形两条直角边的和等于 20,两条直角边各为多少时,这个直角三角形的面积最大?最大值是多少?
答案:
解:设直角三角形的一直角边长为x,则另一直角边长为(20-x),其面积为y,则$y=\frac{1}{2}x(20-x)=-\frac{1}{2}x^{2}+10x=-\frac{1}{2}(x-10)^{2}+50$.当x=10时,$y_{最大}=50$.
∴当两条直角边都为10时,三角形面积最大为50.
∴当两条直角边都为10时,三角形面积最大为50.
7. 将一条长为 20cm 的铁丝剪成两段,并以每一段铁丝的长度为周长各做成一个正方形,则这两个正方形面积之和的最小值是
12.5
$cm^2。$
答案:
12.5
8. 如图,D 是边长为 4 的等边三角形 ABC 的边 BC 上一点,$ ED // AC $ 交 AB 于点 E,$ DF ⊥ AC $ 交 AC 于点 F,$ △EDF $ 的面积最大是(

A.$ 2\sqrt{3} $
B.$ \frac{\sqrt{3}}{2} $
C.2
D.$ \sqrt{3} $
D
)
A.$ 2\sqrt{3} $
B.$ \frac{\sqrt{3}}{2} $
C.2
D.$ \sqrt{3} $
答案:
D
查看更多完整答案,请扫码查看


