《2025年课堂点睛九年级数学上册人教版安徽专版》

1. 下列说法不正确的是(A)
A.直径是圆的对称轴
B.圆既是轴对称图形,又是中心对称图形
C.圆的对称轴有无数条,对称中心只有一个
D.圆围绕着圆心旋转任意角度都能与自身重合

答案： A

2. 如图,⊙O 的半径为 13,弦 AB 的长是 24,ON⊥AB,垂足为 N,则 ON 的长为(A)

A.5
B.7
C.9
D.11

答案： A

3. (宜昌市中考)如图,OA,OB,OC 都是⊙O 的半径,AC,OB 交于点 D,若 AD= CD= 8,OD= 6,则 BD 的长为(B)

A.5
B.4
C.3
D.2

答案： B

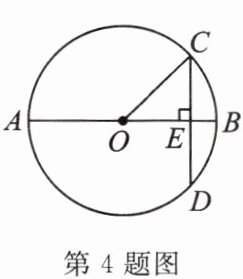
4. 如图,AB 是⊙O 的直径,弦 CD⊥AB 于点 E,CD= 10,BE= 2. 则⊙O 的半径 OC= $\frac{29}{4}$.

答案： $\frac{29}{4}$

5. 如图,AB 为⊙O 的弦,C,D 是直线 AB 上两点,且 AC= BD,求证：∠C= ∠D.

答案： 证明:过点 O 作 OH⊥AB 于点 H.
∵AB 是$\odot O$的弦,
∴AH=BH.
∵AC=BD,
∴AC+AH=BD+BH,即 CH=DH. 又
∵OH⊥AB,
∴OH 垂直平分 CD.
∴OC=OD.
∴∠C=∠D.

6. 往直径为 52cm 的圆柱形容器内装入一些水以后,截面如图所示,若水面宽 AB= 48cm,则水的最大深度为(C)

A.8cm
B.10cm
C.16cm
D.20cm

答案： C

7. (分类讨论思想)已知⊙O 的直径 CD= 10cm,AB 是⊙O 的弦,AB⊥CD,垂足为 M,且 AB= 8cm,则 AC 的长为$2\sqrt{5}cm$或$4\sqrt{5}cm$.

答案： $2\sqrt{5}cm$或$4\sqrt{5}cm$

【变式】已知⊙O 的直径 CD= 10,弦 AB= 8,AB⊥CD,垂足为 M,则 DM 的长为2 或 8.

答案： 2 或 8

8. (西藏自治区中考)如图,AB 是⊙O 的弦,OC⊥AB,垂足为 C,OD//AB,OC= $\frac{1}{2}$OD,则∠ABD 的度数为(D)

A.90°
B.95°
C.100°
D.105°

答案： D

9. (原创题)如图,在⊙O 中,弦 AB= 1,点 C 在 AB 上移动,连接 OC,过点 C 作 CD⊥OC 交⊙O 于点 D,则 CD 的长的最大值为$\frac{1}{2}$.

答案： $\frac{1}{2}$

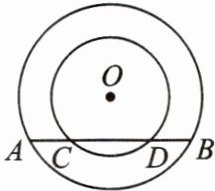
10. (教材第 90 页第 9 题变式)如图,在以点 O 为圆心的两个同心圆中,大圆的弦 AB 交小圆于点 C、D.
(1)求证：AC= BD；
(2)若大圆的半径 R= 10,小圆的半径 r= 8,且圆心 O 到直线 AB 的距离为 6,求 AC 的长.

答案：
(1)证明:过点 O 作 OE⊥AB 于点 E,则 CE=DE,AE=BE,
∴AE-CE=BE-DE,即 AC=BD.
(2)解:连接 OC,OA.
∵OE⊥AB,OE⊥CD,
∴OE=6,
∴CE=$\sqrt{OC^2-OE^2}=\sqrt{8^2-6^2}=2\sqrt{7}$,AE=$\sqrt{OA^2-OE^2}=\sqrt{10^2-6^2}=8$,
∴AC=AE-CE=$8-2\sqrt{7}$.